基本介紹
- 中文名:閔科夫斯基空間
- 別稱:閔科夫斯基時空
- 提出人:H.閔科夫斯基
- 國家:德國
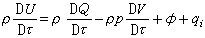












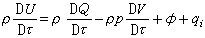












閔科夫斯基空間是物理學上稱為閔科夫斯基時空,它是德國數學家H.閔科夫斯基為適應狹義相對論的需要而提出來的,在古典的時空觀念中,時間和空間是分立的,現實空間...
閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...... 閔科夫斯基泛函是拓撲線性空間上的一類非負值函式,是研究凸集的有效工具。...
在數學中,閔可夫斯基不等式(Minkowski inequality)表明LP空間是一個賦范向量空間。...... 在數學中,閔可夫斯基不等式(Minkowski inequality)表明LP空間是一個賦范...
閔科夫斯基編輯 鎖定 閔可夫斯基(Hermann Minkowski,1864-1909)出生於俄國的Alexotas[1-2] (現在變成立陶宛的Kaunas),但他是德國籍。[2-3] ...
這裡,XU是商空間(X,PU(·))/{x|PU(x)=0},而XV是商空間(X,PV(·))/{x|PV(x)=0}的完備化空間,PU(·)及PV(·)是由U和V各自產生的閔科夫斯基...
閔科夫斯基函式(Minkowski function)是取非負值的次線性函式,這是一類非常重要的凸函式。...
閔科夫斯基維數是一種與閔科夫斯基容度相關聯的維數。閔科夫斯基維數有下列等價定義,這些不同的定義是根據不同的目的引入(故亦有不同的稱呼:布里岡維數,柯...
拓撲線性空間是泛函分析的重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的...零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{...
拓撲線性空間是泛函分析的重要分支,又稱之為拓撲向量空間,它是具有拓撲結構的...零元的每個均衡凸鄰域V的閔科夫斯基泛函pV(x)是E上的連續半範數。反之,設{...
介紹 閔科夫斯基矩陣(Minkowski matrix)一類實方陣.1}7科夫斯基矩陣應滿足條件:a;;}0(i}j),且各階主子式滿足}a;; })0. ...
閔科夫斯基的主要論著有《數的幾何》(1896),《算術等價的不連續性》(1905),《丟番圖逼近》(1907),《時間與空間》(1907),《兩篇關於電動力學基本公式的論文...
閔科夫斯基上限(Minkowski bound)界定理想數個數的上限.若F,為n次數域(即Q的n次擴張),d為其判別式,則F.的閔科夫斯基上限為 式中2rZ為F到C的虛嵌入個數....
自反局部凸空間(reflexive locally convex space)屬於一類局部凸空間,也是屬於具有...零元的每個均衡凸鄰域V的閔科夫斯基泛函 pv(x) 是E上的連續半範數。反之,...
閔科夫斯基幾何是一種非歐幾何,它建立在洛倫茲變換之上。因為它是一種非歐幾何,因此很多典型歐幾里得幾何結論不成立。它在相對論研究中占有重要地位。 ...
伴隨著對電磁理論與引力場的深入研究,人們的時空觀念發生了根本的變化,這使得閔科夫斯基空間和黎曼空間(用現代術語說,洛倫茨流形)的幾何學成為愛因斯坦狹義相對論和...
古典的局部微分幾何是研究三維歐氏空間E3的曲線和曲面在一點鄰近的性質,它的發展...而從閔科夫斯基時空到洛倫茨流形只經過十年時間,這是因為黎曼幾何學的張量分析...
20世紀初,對電磁理論和引力場的研究,使閔科夫斯基空間和黎曼空間的幾何大大發展,成為愛因斯坦狹義相對論和廣義相對論的基礎。許多物理量以向量、張量和旋量作為...
19世紀以來高維研究興起,如閔科夫斯基空間就是三維歐氏空間加上時間變數的四維空間。1878年德國數學家G.康托爾證明了一條線段上的點能夠和正方形的點建立一一對應...
同時,這也否定了牛頓的絕對空間和絕對時間,並通過光速不變原理把一維時間和三維空間聯繫了起來,成為相互聯繫的四維時間-空間。H閔科夫斯基首先發現了這一性質,因而...
伴隨著對電磁理論和引力場的深入研究,人們的時空觀念發生了根本的變化,這使得閔科夫斯基空間和黎曼空間的幾何學成為愛因斯坦狹義相對論和廣義相對論所必需的數學理論...
這一思想最初得益於數學大師閔科夫斯基的數學理論,閔科夫斯基認為單純的時間與單純的空間在被統一起來後,可以作為一種實體而存在,愛因斯坦的引力解說就是建立在這...
