復歐幾里得空間是一種帶非退化對稱雙線性函式的複線性空間,簡稱復歐氏空間,是通常歐氏空間的推廣。
基本介紹
- 中文名:復歐幾里得空間
- 外文名:complex Euclidean space
- 適用範圍:數理科學
簡介
意義
相關概念
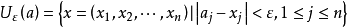
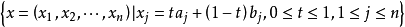
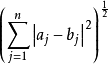
復歐幾里得空間是一種帶非退化對稱雙線性函式的複線性空間,簡稱復歐氏空間,是通常歐氏空間的推廣。
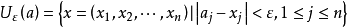
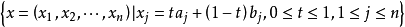
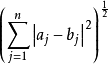
復歐幾里得空間是一種帶非退化對稱雙線性函式的複線性空間,簡稱復歐氏空間,是通常歐氏空間的推廣。...
完備的內積空間稱為希爾伯特空間,希爾伯特空間的概念還可以推廣到複線性空間上。...n維歐幾里得空間的推廣,可視為“無限維的歐幾里得空間”,是泛函分析的重要研究對象...
黎曼空間是一種非歐幾里得空間,是彎曲空間,也是一種度量空間,具有不變的線元ds2=gikdxidxk,其中,作為廣義坐標(x0,x1,…,xn)函式的gik,稱為黎曼度規,是個二...
四維空間不同於三維空間,四維空間指的是標準歐幾里得空間,可以拓展到n維;四維時空指的是閔可夫斯基空間概念的一種誤解。人類作為三維物體可以理解四維時空(三個空間...
歐幾里得幾何是在約公元前300年,由古希臘數學家歐幾里得建立的角和空間中距離之間聯繫的法則。歐幾里得首先開發了處理平面上二維物體的“平面幾何”,他接著分析三維...
的基域.當P是實數域時,V稱為實線性空間.當P是複數域時,V稱為複線性空間。...最早提出多維歐幾里得空間的系統理論。1844—1847年,他與柯西(Cauchy,A.-L.)...
在數學裡,希爾伯特空間即完備的內積空間,也就是說一個帶有內積的完備向量空間。是有限維歐幾里得空間的一個推廣,使之不局限於實數的情形和有限的維數,但又不失...
在數學裡面,內積空間是增添了一個額外的結構的向量空間。這個額外的結構叫做內積,或標量積,或點積。這個增添的結構允許我們談論向量的角度和長度。內積空間由歐幾里得...
它不僅是微分幾何的基礎,也套用在微分方程、變分法和複變函數論等方面。...康德曾經說過:“歐幾里得幾何是人類心靈內在固有的,因而對於‘現實’空間客觀上是...
泰希米勒空間,是指黎曼曲面復結構的形變所組成的空間。理論主要是用擬共形映射為工具來研究黎曼曲面的模問題,這種研究與克萊因群以及低維拓撲問題有一定的聯繫。...
這種拓撲嚴格地細於上面定義的歐幾里得拓撲;在這種拓撲空間中,一個點列收斂於一點,若且唯若,該點列在歐幾里得拓撲中也收斂於這個點。這樣我們就給出了一個集合...
[2] 五維空間是一種經常在數學中出現的抽象概念。在物理學和數學中,N數字的序列可以理解為表示N維歐幾里得空間中的位置。 宇宙的維度是否為五維同時也是個辯論的話...
歐幾里得空間 上的速降函式空間 是滿足以下條件的函式的集合:其中α, β 是多重指標,C∞( ) 是所有從 射到C 的光滑函式。其中sup符號指函式的最小上界, 指...
閔科夫斯基為適應狹義相對論的需要而提出來的,在古典的時空觀念中,時間和空間是分立的,現實空間的模型是三維的歐幾里得空間,時間是一維的數軸,兩個事件的同時性是...
三維空間,日常生活中可指由長、寬、高三個維度所構成的空間。而且日常生活中使用的“三維空間”一詞,常常是指三維的歐幾里得空間。在歷史上很長的一段時期中,...
在數學中,特別是在微分幾何和代數幾何中,復流形是具有復結構的微分流形,即它能被一族坐標鄰域所覆蓋,其中每個坐標鄰域能與n維復線性空間中的一個開集同胚,從而...
復曲率直觀幾何表示 編輯 當一個點的標量曲率為正時,圍繞該點的小球的體積比歐幾里得空間中具有相同半徑的球的體積更小。另一方面,當一個點的標量曲率為負時,小球...
