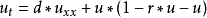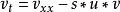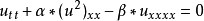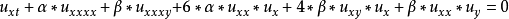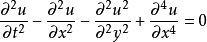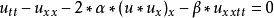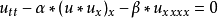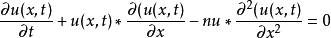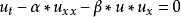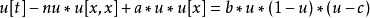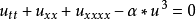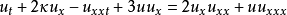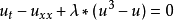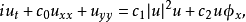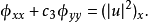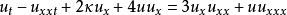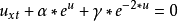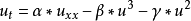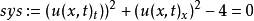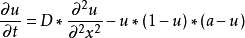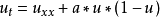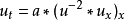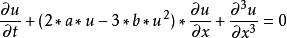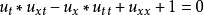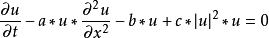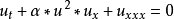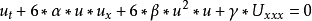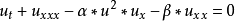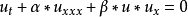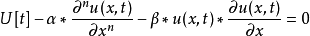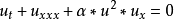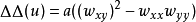非線性偏微分方程

非線性偏微分方程是各階微分項有次數高於一的微分方程即為非線性偏微分方程，是現代數學的一個重要分支，無論在理論中還是在實際套用中，非線性偏微分方程均被用來描述力學、控制過程、生態與經濟系統、化工循環系統及流行病學等領域的問題。

基本介紹

• 中文名：非線性偏微分方程
• 外文名：Nonlinear partial differential equation 
• 理論基礎：極限理論
• 對立：線性偏微分方程
• 主要貢獻人：牛頓
• 縮寫：NLPDE

發展情況

目前微分方程研究的主體是非線性微分方程，特別是非線性偏微分方程(NLPDE)。很多意義重大的自然科學和工程技術問題都可歸結為非線性偏微分方程的研究。現實生活的許多領域內數學模型都可以用NLPDE來描述，很多重要的物理、力學等學科的基本方程本身就是NLPDE。另外，隨著研究的深入，有些原先可用線性微分方程近似處理的問題，也必須考慮非線性的影響，所以對NLPDE的研究，特別是NLPDE求解精確解的研究工作就顯示出了很重要的理論和套用價值，但是數學研究的結果，在目前還未能提供一種普遍有效的求精確解的方法.20世紀50年代以來，人們對非線性現象的研究中提出了“孤子”的概念，進而使得對NLPDE求解的研究成為非線性科學中的熱點。

研究內容

利用非線性偏微分方程描述上述問題充分考慮到空間、時間、時滯的影響，因而更能準確的反映實際。本方向主要研究非線性偏微分方程、H-半變分不等式、最優控制系統的微分方程理論及其在電力系統的套用。

1.非線性偏微分方程的研究：我們主要研究偏微分方程解的存在唯一性（和多解性）及穩定性；偏微分方程的初值問題、初邊值問題的整體解（包括周期解和概周期解）的存在性及漸近性；平衡解的存在性，尤其是當問題依賴於某些參數時平衡解的分叉結構，以及平衡解的穩定性問題；非線性方程的數值解。

2．H－半變分不等式的研究：建立具有極大單調運算元擾動的多值（S）型和偽單調型映象的廣義度理論，廣義不動點指標理論和具有非凸、不可微泛函的非線性發展型H－半變分不等式理論，由此來研究含間斷項的非線性偏微分方程。

3．最優控制系統的微分方程理論及其在電力系統的套用：主要研究與電力生產有關的控制系統的理論和套用。首先提出了對Banach空間中抽象非線性發展方程所描述的最優控制系統的研究。引進非光滑分析，研究最優控制系統的微分方程，利用變分不等式理論研究多值問題、數值計算等，所獲理論成果套用於電力系統的許多最優控制問題（如：電力系統勵磁調節器傳遞函式的辨識、牛頓最優潮流的數學模型等）。

定義

非線性偏微分方程(NLPDE)，又稱非線性數學物理方程、非線性演化方程。它是描述現代諸多科學工程領域如物理化學、生物，大氣空間科學等中的非線性現象的數學模型。

函式是一個廣義的偏微分方程，如果 u，v 是此微分方程的兩個解，而（au+bv) 也是此微分方程的解，則此偏微分方程則為線性偏微分方程，否則為非線性偏微分方程。

求解方法

精確求解非線性發展方程的工作具有重複性、固定的套路和規律、計算量大的特點，計算機代數的出現使人們擺脫了刻板、大量而重複的計算，提高了速度保證了準確率。年來在齊次平衡原則下又發展了多種求解非線性偏微分方程精確解的方法：像Tanh一函式法，Sine一Cosine方法，Jacobi橢圓函式展開法，Riccati方程方法及F一展開法等。這些方法一般都藉助於計算機代數系統(Mathematica或Maple)，求解方便、直接，而且可以對解進行數值模擬以便於直觀分析解的性質。

• 逆算符法
  該方法是收斂的，而且收斂速度相當快，能夠得到精確解。
  
• 齊次平衡法
  該方法將非線性發展方程的求解問題轉化為純代數運算。利用這種方法不僅可以得到方程的Backlund變換，而且能得到非線性偏微分方程的新解。
  
• Jacobi橢圓函式方法
  該方法此方法包含了雙曲正切函式展開法。
  
• 輔助方程方法
  
• F-展開法
  
• 雙曲正切函式展開法
  

常見方程

名稱	方程
班傑明-小野方程
別洛烏索夫-扎伯廷斯基方程	,
班傑明-小野方程
波格雅夫連斯基-科譳普勒琛科方程
玻恩-英費爾德方程
博欣內斯克方程
博欣內斯克型方程
非規範博欣內斯克方程
伯格斯方程
伯格斯-費希爾 方程
變形伯格斯方程
非規範伯格斯方程
伯格斯-赫胥黎方程
布雷瑟頓方程
卡馬薩-霍爾姆方程
查菲 - 堙方特方程
查普里金方程
戴維-斯圖爾森方程組
DP 方程
多德-布洛-米哈伊洛夫方程
非線性擴散方程
迪姆方程
程函方程
埃斯特韋斯-曼斯菲爾德-克拉克森方程
菲茨休 - 南雲方程
費希爾方程
藤田-斯托姆方程
加德納方程
吉本斯-查理夫方程
金茲堡－朗道方程
亨特 - 薩克斯頓方程
伊藤方程
KdV方程
MKdV方程
KdV-mKdV方程
KdV-Burgers方程
變形KdV-Burgers方程
非規範KdV方程
廣義伯格斯-KdV方程
非規範變形KdV方程
馮·卡門方程

套用

研究方向

1. 變分不等式理論與能量泛函的凸性密切相關，由於現代科學技術的需要，特別是研究自由邊界和固體力學問題的需要，傳統的方法往往都無法解決這類問題，人們對H-半變分不等式進行研究，研究涉及現代分析及套用、偏微分方程以及科學計算等眾多領域中亟待解決和發展的重要課題。

2．該研究是現代數學與電力生產的交叉學科研究課題，它對電力生產及管理有著十分重要的理論指導意義和實際套用價值，為控制系統設計、分析和計算都可提供一些重要的理論依據。在套用數學學科的這一研究領域中本課題屬於國內外前沿性研究工作。

突破

1．深入研究空間、時間、時滯對解的性質的影響，諸如靜態解、周期解的存在性、解的存在性、漸近性等問題；尋求它們在含間斷項的非線性偏微分方程方面的突破。

2．尋求和發現新的處理非單調、非凸不可微能量泛函的方法（如建立Ishikawa疊代序列收斂準則），建立發展型方程G－收斂準則，尋求可行的光滑方法將運算元方程光滑化，創建新的先驗估計方法。

3．套用現代數學所獲得的理論，研究最有控制系統的微分方程，為控制系統設計、分析和計算提供一些重要的理論依據和方法。