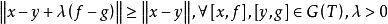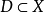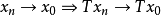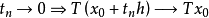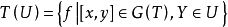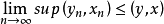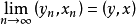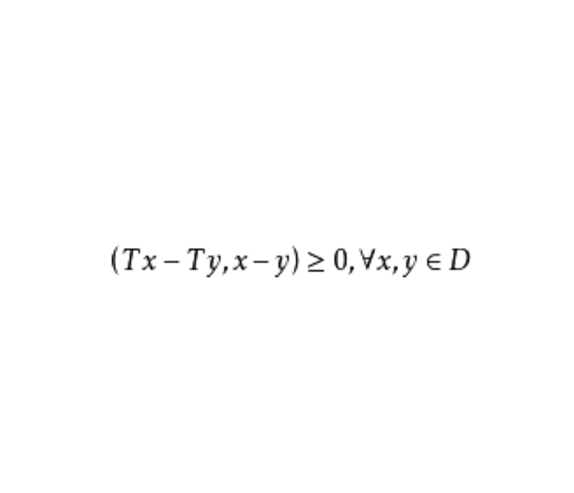單調運算元(monotonic operator)的概念起源於可微凸泛函的導數。設φ是在B空間X上定義的這種函式,則 <φ'(x)-φ'(y),x-y>≥0,對任意的x,y∈X,其中<,>表示X'與X之間的對偶。直線上的可微凸函式的導函式是單調不減的,於是就把滿足特定條件的運算元T:X→X' ,稱為單調運算元,如果α>0則稱為強單調運算元。自反B空間上弱線段連續的強單調運算元是 X→X* 的滿射(所謂弱線段連續,指對任意的x,y∈X,T(x+ty)→T(x)當 t→0)。這個滿射性定理是G.J.明蒂、F.E.布勞德給出的,它在非線性運算元半群理論、非線性發展方程以及一類非線性橢圓型方程的存在性理論中經常用到。
基本介紹
- 中文名:單調運算元
- 外文名:monotonic operator
- 起源:可微凸泛函的導數
- 類型:導數
- 學科:數學
- 屬於:非線性運算元
單調運算元的概念
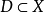
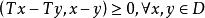
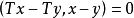
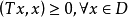
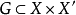
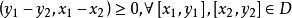
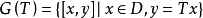
單調運算元的基本性質