最優控制系統,是指針對某一系統特定的被控對象建立數學模型,選擇一個容許的控制律,使得被控對象按預定要求運行並使給定某一性能指標達到極大值(或極小值)的系統。
基本介紹
- 中文名:最優控制系統
- 外文名:Optimal Control Systems
- 相關領域:控制理論、自動化
基本概念
最優控制
最優控制系統
變分學
分析方法
極大值原理
動態規劃
套用類型
積分型性能指標
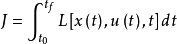
末值型性能指標
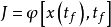
複合型性能指標
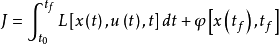

最優控制系統,是指針對某一系統特定的被控對象建立數學模型,選擇一個容許的控制律,使得被控對象按預定要求運行並使給定某一性能指標達到極大值(或極小值)的系統。
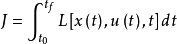
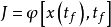
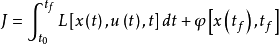
最優控制系統,是指針對某一系統特定的被控對象建立數學模型,選擇一個容許的控制律,使得被控對象按預定要求運行並使給定某一性能指標達到極大值(或極小值)的系統...
最優控制是現代控制理論的核心,它研究的主要問題是:在滿足一定約束條件下,尋求最優控制策略,使得性能指標取極大值或極小值。...
最優控制理論(optimal control theory),是現代控制理論的一個主要分支,著重於研究使控制系統的性能指標實現最最佳化的基本條件和綜合方法。 最優控制理論是研究和解決...
最速控制系統,又稱快速控制系統。是能以最短時間完成規定控制作用的最優控制系統。...... 能以最短時間完成規定控制作用的最優控制系統,又稱快速控制系統。例如,...
以離散系統為被控對象的最優控制系統。...... 離散系統被控對象的最優控制系統 簡介如果被控對象是連續系統,則通過離散化的處理後,也可按離散最優控制方案來設計...
《最優控制系統的微分方程理論》是1989年出版的圖書,作者是張學銘。本書內容微分方程預備知識,線性系統的最優控制,龐特里雅金的最大值原理及證明,最優控制的近似...
自適應最優控制(Adaptive optimal control )是指根據控制對象本身參數或周圍環境的變化,自動調整控制器參數以使控制系統的性能指標實現最最佳化的基本條件和綜合方法,...
線性最優控制是最優控制的一個特殊類,它的實質是要找出允許的控制作用(規律),使得動態系統(受控對象)從初始狀態轉移到某種要求的終端狀態,並且保證某種要求的性能...
本書是工科院校自動控制類各研究方向的碩士研究生和高年級本科生的“最優控制”課程教材。基本內容有:變分法、連續系統最優控制、線性連續系統的二次型調節器(LQR...
在計算機科學中,次優控制系統是指在最優控制系統的設計中,由於採用了簡化方法,而性能指標未達到最優值的控制系統。特別是對於大系統,由於大系統具有維數高、非...
最優控制理論基礎是普通高等教育“十一五”國家級夫劃教材,由呂顯瑞著作,黃慶道編著。...
最優控制方法是對一個因果關係鏈偶合系統的運行過程施加控制以獲得最優的運行效果所使用的理論和方法體系。...
《最優控制的理論與方法》是一本書籍,出版時間1989年,作者吳滄浦。該書講解了參量系統的最優控制的理論和方法,重點闡述確定性系統的最優控制。...
《最最佳化方法與最優控制》是哈爾濱工程大學出版社出版的圖書,作者是王曉陵、陸軍。本書可作為高等工業院校自動化、測控技術與儀器、電氣工程及其自動化等相關專業的...
非線性最優控制(Nonlinear optimal control)實質是要找出允許的控制作用(規律),使得動態系統(受控對象)從初始狀態轉移到某種要求的終端狀態,並且保證某種要求的性能...
H∞最優控制,簡而言之,就是用H∞範數作為日標函式的度量邊行最佳化設計。H∞範數是定義在Hardy空間 上的範數,在H∞控制理論中是指在S右半平面上解析的有理函式...
《最優控制的結構化理論》是1999年9月冶金工業出版社出版的圖書,作者是高學東。...... 著有《最優控制的結構化理論》、《管理信息系統教程》、《高維稀疏聚類知...
隨機最優控制(Stochastic optimal control)是指選擇控制變數,使隨機系統某個性能指標達到最優的控制。在隨機系統控制中,必須進行狀態估計。套用不同的狀態估計方法,會...
最優控制算法用以定出最優控制(見最優控制理論)的具體形式的計算方法。...... 中利用搜尋尋優或梯度尋優技術和牛頓-拉夫森方法等直接求解非線性系統最優控制問題...
《套用最優控制》是1988年西安交通大學出版社出版的圖書,作者是吳受章。本書是工科院校自動控制類型各研究方向的碩士研究生的“最優控制”教材。...
《最優控制理論與方法》是2002年出版的圖書,作者是荊海英。本書主要介紹了最優控制理論的三種方法,即變分法、最大值原理與動態規劃方法。...
《系統最最佳化及控制》是1998年機械工業出版社出版的圖書,作者是符曦。...... 《系統最最佳化及控制》是1998年機械工業出版社出版的圖書,作者是符曦。...
《最優控制方法及其套用》是2012年四川大學出版社出版的圖書。...... 書中結合算法給出最優控制問題的大量實例,包括空間技術、工程問題、經濟計畫和管理信息系統的應...
《最優控制》是大連海事大學出版社2014年出版的圖書,沈智鵬主編。...... 本書共六章,第一章結合實例分析最優控制問題的數學描述、系統性能指標等最優控制問題的相...
自然系統包括生態平衡系統、生命機體系統、天體系統、物質微觀結構系統以及社會系統...信息交換和自動控制等功能進行分析研究,藉以達到最最佳化設計,最優控制和最優管理...
《最優控制理論及其套用》是2010年大連理工大學出版社出版的圖書,作者是錢偉懿。...... 《最優控制理論及其套用》從理論及工程套用的角度,系統地介紹了最優控制理論...
《最最佳化與最優控制》是2009年2月1日西安交通大學出版社出版的圖書。本書作為西安交通大學“十一五”規劃教材主要講述了最最佳化與最優控制的基本理論與方法。...
《最優控制理論、方法與套用》是2011年高等教育出版社出版的圖書,作者是王青,陳宇。...
