在計算機科學中，次優控制系統是指在最優控制系統的設計中，由於採用了簡化方法，而性能指標未達到最優值的控制系統。特別是對於大系統，由於大系統具有維數高、非線性、遞階和分散結構以及時滯等複雜性，若採用精確的最優控制，則會帶來過大的計算量，甚至不可能實現。因此需要採用模型降價、結構分解、線性近似或參數靈敏度展開等簡化方法。這些簡化的代價就使性能指標產生一定程度的退化。
基本介紹
- 中文名：次優控制系統
- 外文名：Suboptimal control system
- 方法：採用了簡化方法
- 含義：性能指標未達到最優值
- 使用設計：最優控制系統的設計
- 學科：控制工程、計算機科學
概述,線性二次型次優控制系統與最優控制系統,最優控制系統,線性二次型次優控制,大系統理論,隨機控制系統,
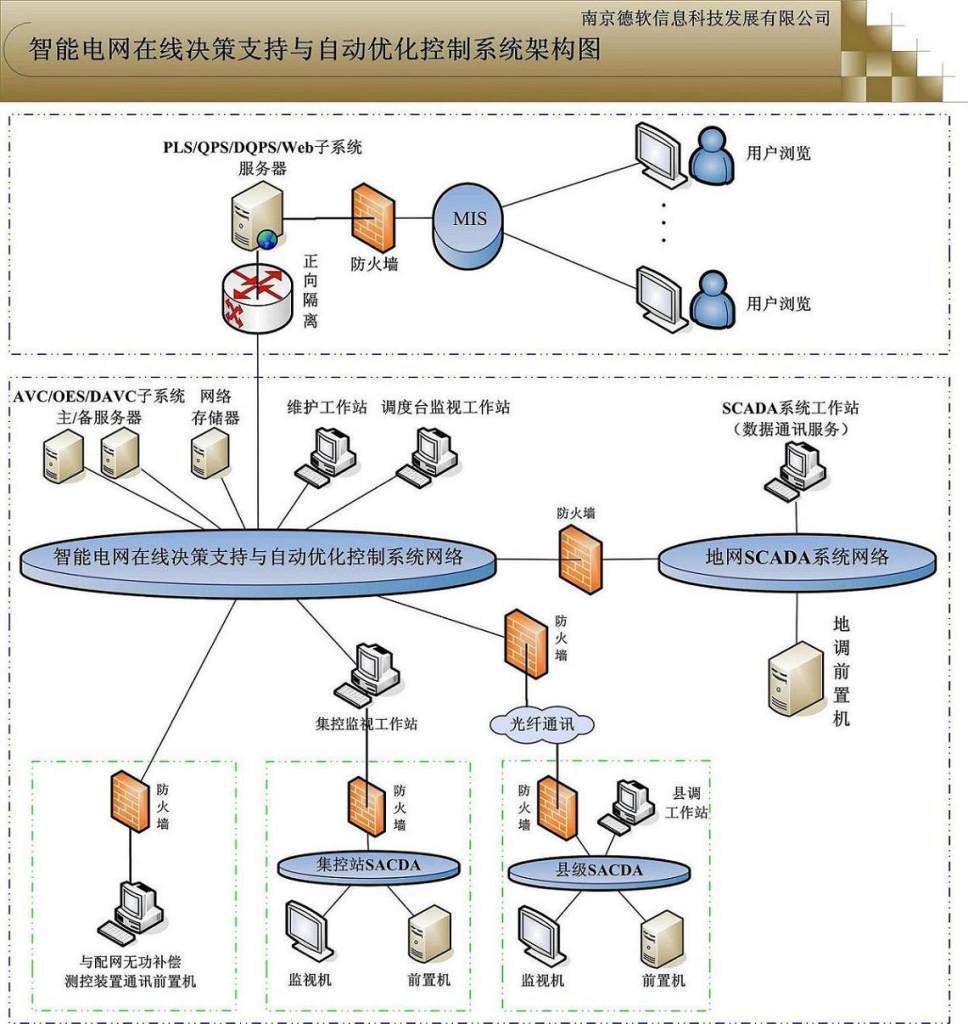
概述
控制系統是指由控制主體、控制客體和控制媒體組成的具有自身目標和功能的管理系統。控制系統意味著通過它可以按照所希望的方式保持和改變機器、機構或其他設備內任何感興趣或可變的量。控制系統同時是為了使被控制對象達到預定的理想狀態而實施的。控制系統使被控制對象趨於某種需要的穩定狀態。在計算機科學中，次優控制系統是指在最優控制系統的設計中，由於採用了簡化方法，而性能指標未達到最優值的控制系統。主要是因為這類系統中多數控制對象的數學模型隨時間和工作環境的改變而變化，其變化規律事先往往不知道。
對於大系統，由於具有維數高、非線性、遞階和分散結構以及時滯等複雜性，若採用精確的最優控制，則會帶來過大的計算量，甚至不可能實現。因此需要採用模型降價、結構分解、線性近似或參數靈敏度展開等簡化方法。這些簡化的代價就使性能指標產生一定程度的退化。對於隨機系統、分布參數系統、非線性系統等也常常需要採用次優控制設計。
線性二次型次優控制系統與最優控制系統
最優控制系統
最優控制系統是指在一定具體條件下，完成所要求控制任務時，系統的某種性能指標具有最優值的控制系統。如在整個控制過程中，誤差達到極小(即最優值)的系統。若控制系統主要任務是維持平衡狀態恆定，這種系統就是最優鎮定系統(或最優調節系統);若控制系統主要是以最小誤差跟蹤運動目標、希望的軌跡或控制輸入的變化，這就是最優隨動(或跟蹤)系統。
線性二次型次優控制
使用二次型性能指標的線性定常系統次優控制或準最優控制。線性二次型最優控制要求使用全部狀態變數反饋，因為最優控制應該由反映系統內部狀態的全部信息參與組合。但在工程實際中，並非所有的狀態變數都是能夠測取或易於測取的。例如，最優控制規律為u*=Kx，x是狀態向量，u*是最優控制，但矩陣K的元素不是都能自由選擇的。還由於系統在物理方面的約束，某些增益被固定了，相對缺少靈活性。再者，全部狀態可能不能都被取來供反饋，而必須構造狀態觀測器，相對而言複雜性加大。
這樣，就出現了次優控制問題。這時，只使用能夠取到的狀態變數實施反饋，反饋矩陣K的某些元素則是受約束的。這樣，達不到“最優”，只能是“次優”。
大系統理論
研究大型、高階、複雜系統的科學。大型一般指系統可分為相互耦合的若干個子系統; 高階一般指不可能用常規方法進行時域或頻域分析的系統; 複雜一般指系統具有多級結構、多個控制中心，相互關連控制，信息結構各異的系統。它是控制論在實踐需求下的新發展，以適應新的套用領域的新理論、新方法。它研究在自然科學、社會科學、經濟科學、生物科學等領域所提出的大系統的控制問題。
從自動控制發展史上看，前期研究中心是集中控制的反饋控制系統。一個被控對象，其輸出變數經測量饋送給集中的一個控制器上，控制器按預定的控制要求經運算產生控制信號，再饋送給控制對象，從而使控制對象的輸出變數按要求變化。隨著控制變數的增多，集中控制變得越來越困難，因為“決策人”或控制器能處理的信息容量是有限的，對於某個確定的目標，一個“決策人”或控制器要理解它都嫌太複雜，更不用說控制了，這樣，就必然發展成分散控制，也就是說一個控制對象由多於一個“決策人”或控制器進行控制。每個“決策人”只控制局部系統，稱之為子系統。各子系統之間必然是相互關連的，這樣，就出現了子系統之間的耦合問題。早期提出的問題是各子系統既然是分散控制的，最好它們互相獨立或至少是相對獨立的，有耦合也是弱耦合的，這就是“解耦”問題 (decompose problem)。丹京和沃爾夫 (G.Dantzing and P.Wolf) 於1960年首先提出解耦的數學理論，錢學森也提出了“相互獨立控制”的一般方法，也就是解耦控制方法，何毓琦和米特 (Ho Y.C. and S.K.Mitter) 於1976年提出了新的解耦方法，後來有很多學者發展了解耦理論。即使各子系統可完全解耦亦需在各子系統間交換信息，解耦是有條件的，不是所有情況皆能完全解耦，各子系統間就需要交換信息，這就又出現新的困難： 各子系統之間平行的交換信息量過大，從而使信息交換效率不高，時間也來不及，這就使分散控制實時性不能實現。一般時間離散 (時間分割、採樣系統) 控制，要在一個採樣周期內完成全部信息交換，才認為是實時的。當子系統多，信息交換量大時，這一實時性條件就得不到滿足，單純分散控制就困難了。按照整個目標的要求，為了協調分散的“決策人”的活動，設定專門的協調職務構成等級遞階，比所有“決策人”之間進行聯繫，效率要高得多，信息通道也少得多，這就是分散遞階結構。例如在電網控制中，每個電站是一個子系統，整個電網連線著多個電站和用戶; 統一設一個協調級來協調各電站和用戶，一個國家統一協調各省市，各省市是子系統; 一個人由大腦統一協調各局部，心、肝、脾、胃、腎是子系統，眼、耳、鼻、口、皮是感覺子系統，手、腳是執行子系統，構成分散遞階控制 (Decen tralized hierarchical control)。這種分散遞階控制不能用集中控制理論和方法進行分析設計，也不僅是解耦控制問題，它需要新的理論方法。更複雜的系統常是一些子系統組成“聯盟”，有自己的協調級，各協調級之上再設組織級，從而構成三級結構。
大系統理論主要研究內容：①大系統的建模理論，控制理論;②大系統的結構理論。分散遞階結構即是實際系統最合理的結構，因此它也是最有生命力、最有發展前途的結構，它的理論和套用將大有發展。
特點
大系統沒有嚴格的數學定義.文獻中研究的大系統有如下特點：
1.規模龐大.通常系統中含有許多小系統，或跨越很大空間。
2.結構複雜.各小系統可能分級，控制採用的信息可分散，也可集中，分散信息又可分為完全分散或部分分散等。
3.功能綜合.對一個大規模系統性能的評價是多指標、綜合性的，大規模系統必須具備各種功能才能達到預期性能。大小和複雜程度是個相對概念，隨著科學技術的發展，對大規模系統的理解也可能發生變化。
隨機控制系統
受隨機因素影響的動態系統.通常用隨機微分方程或隨機差分方程來描述.從控制理論的角度來看，對隨機系統的研究主要包括下列方面內容：
建模與辨識.從量測數據建立系統的數學模型，或已給出系統的模型結構，根據量測數據來估計模型中的未知參數.。濾波。根據量測數據及系統的模型，估計受到噪聲干擾的系統狀態或信號。
隨機控制。對隨機系統構造控制，使給定的性能指標達到極小。
隨機適應控制.對隨機系統一方面辨識系統，估計參數，同時又給出控制，使性能指標達到最小。
具體來講，在建模與辨識方面，對量測到的隨機數據，常用白噪聲驅動差分方程(ARMA過程)來建模.對ARMA過程的係數、階次等的估計稱時間序列分析，它已有一套較成熟的方法，但能用這種方法有效處理的過程通常要有平穩性，而反饋控制系統，由於控制項的作用，系統的輸出過程一般不具有平穩性，所以常用的時間序列分析方法對反饋控制系統的參數估計並不適用.對隨機控制系統建模時最常用的模型是ARMAX過程，對它的係數估計通常用最小二乘、極大似然或由此引申出來的其他算法來估計，但要使估計收斂到真值，就得要求系統受到一定程度的激勵.但這種激勵要多大，收斂速度有多快，這就引發了許多研究.對反饋控制系統的階估計是一個饒有興趣的問題。
在隨機控制方面，對部分觀測的系統，狀態不能精確地量測，最多只能得到它的濾波值，這時一個直觀的想法是用狀態濾波值來取代相應確定性系統(即把噪聲取為零)最優控制中的狀態變數，稱為必然等價控制。但這樣的控制未必就是最優隨機控制.一個重要的例外是線性二次高斯(LQG)問題，對它的必然等價控制正是最優隨機控制.對ARMAX系統，就不用濾波，對常見的LQ、跟蹤、模型參考等問題均可得到最優隨機控制。但一般說，只有線性系統，並只對有限的幾種性能指標，才能得到最優隨機控制.對非線性系統，除了極個別例外，不易得到最優隨機控制的顯式表達.用次優控制逼近，是一個有效的方法.隨機極大值原理，雖有一定指導意義，但難於套用。
在隨機適應控制中，已有的結果主要集中在完全觀測的隨機控制系統，它要求一邊估計系統參數，一邊設計隨機控制.如果系統又是部分觀測的，那么還要加濾波.三項任務要同時完成，至今還未見到一個完整的結果.對ARMAX系統的適應LQ問題、適應鎮定、適應模型參考等問題，都已有理論上嚴格的結果.特別是適應跟蹤，它在工程實際中已有廣泛套用，其收斂性和最優性證明也已經解決。
由於工程技術、環境生態、社會經濟等領域中出現的實際系統，一般都帶有隨機干擾，所以對隨機系統的研究為實際套用的必須，但也帶來許多艱深的理論課題，所以長期以來，隨機控制系統受到各種背景研究者的廣泛關注。
