目標
隨機控制理論的目標是解決隨機控制
系統的分析和綜合問題。維納濾波理論和卡爾曼-布希濾波理論是隨機控制理論的基礎。卡爾曼濾波是一種高效率的
遞歸濾波器(自回歸濾波器), 它能夠從一系列的不完全及包含
噪聲的
測量中,估計
動態系統的狀態。
內容
控制理論中把隨機過程理論與
最優控制理論結合起來研究隨機系統的分支。隨機系統指含有內部隨機參數、外部隨機干擾和觀測噪聲等隨機變數的系統。隨機變數不能用已知的時間函式描述,而只能了解它的某些統計特性。
自動控制系統分為確定性系統和不確定性系統兩類,前者可以通過觀測來確定系統的狀態,後者則不能。
隨機系統是不確定性系統的一種,其不確定性是由隨機性引起的。嚴格地說,任何實際的系統都含有隨機因素,但在很多情況下可以忽略這些因素。當這些因素不能忽略時,按確定性控制理論設計的控制系統的行為就會偏離預定的設計要求,而產生隨機偏差量。
涉及領域
飛機或飛彈在飛行中遇到的陣風,在空間環境中衛星姿態和軌道測量系統中的測量噪聲,各種電子裝置中的噪聲,生產過程中的種種隨機波動等,都是隨機干擾和隨機變數的典型例子。隨機控制系統的套用很廣,涉及航天、航空、航海、軍事上的火力控制系統,工業過程控制,經濟模型的控制,乃至生物醫學等。
研究課題
隨機控制理論研究的課題包括隨機系統的結構特性和運動特性(如動態特性、
能控性、
能觀測性、
穩定性)的分析,隨機系統狀態的估計,以及隨機控制系統的綜合(即根據期望性能指標設計控制器)。隨機系統中含有隨機變數,所以在研究中需要使用隨機過程的基本概念和機率統計方法。嚴格實現隨機最優控制是很困難的。
對於線性二次型高斯(LQG)隨機過程控制問題,包括它的特例最小方差控制問題,可以套用
分離原理把隨機最優控制問題分解成
狀態估計問題和確定性最優控制問題,最終能得到全局最優的結果。但對於一般的隨機控制問題套用分離原理只能得到次優的結果。
隨機狀態模型
隨機系統在連續時間情形下的動態過程,常可用隨機微分方程
描述,式中
x(
t)為狀態向量,d
x(
t)為由時刻
t至
t+d
t狀態的增量,
u(
t)為控制輸入,
θ為隨機參數,
w(
t)為獨立增量隨機過程,其微分d
w(
t)可理解為白噪聲。在離散時間情形下的動態過程則可採用隨機差分方程
 隨機微分方程
隨機微分方程描述。式中
t=0,1,2,…為離散時間變數,
w(
t)為獨立白色噪聲序列。兩種情況下系統的輸出方程都為:
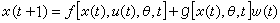 隨機差分方程
隨機差分方程y(
t)=
h【
x(
t),
θ,t】+
v(
t)
隨機最優控制
分析
使隨機控制系統的某個性能指標泛函取極小值的控制稱為隨機最優控制。由於存在隨機因素,這種性能指標泛函需要表示為統計平均(求數學期望)的形式:
式中
E{·}表示{·}的均值即數學期望。使性能指標
J為極小的最優控制常可取為開環和反饋控制兩種形式。如果控制過程中決定
u(
t)所依據的只是設計時過程特性和隨機變數的信息,沒有進一步的測量和更新,這種控制策略就稱為是開環的。若在決定
t時刻的控制作用
u(
t)時可以直接利用τ時刻的實時測量值
y(τ),則稱控制
u(
t)具有反饋形式,其中要求τ≤
t,這是因果性或物理可實現性所要求的。
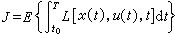 統計平均
統計平均按照利用實時信息的充分程度,又可把反饋形式的控制策略分為兩種情形。當只利用這些信息來控制狀態變數,而沒有通過實時觀測來估計和改進各隨機變數的統計特性並修改控制策略時,這種策略稱為是被動反饋式(簡稱反饋式)的。若控制策略兼有上述“控制”和“估計”兩種功能並具有自行修正的能力,則稱為閉環策略(或主動反饋策略)。這種“反饋”和“閉環”的差別是不確定性控制問題所特有的。
A.A.費爾德包姆最先指出閉環隨機最優控制策略的這種雙重功能,並稱之為二重最優控制。閉環(或二重)最優策略可達到在已有信息條件下的最好品質或全局最優解。同時它還具有不斷按照實時測量改進對不確定性的認識並修正策略的功能,也稱為隨機自適應最優控制。閉環最優控制的求解很困難,通常只能根據最優解的定性性質來構造次優解。只對某些特殊問題才可能給出定量解法。
重要性質
隨機最優控制有兩個重要的性質。由於存在不確定性,控制作用常寧可取得弱一些,保守一些。這稱為謹慎控制。另一方面為更好和更快地進行估計,必須不斷激發系統中各種運動模式,為此需要加入一些試探作用。試探作用的大小,則根據增加的誤差、直接費用和所帶來的好處等因素加以折衷權衡進行選擇。謹慎和試探已成為設計隨機控制策略的兩個重要原則。
問題舉例
線性 (Linear)二次型 (quadratic)高斯(Gaussian)隨機過程控制 線性差分方程
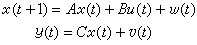 線性差分方程
線性差分方程問題是用途最廣的且可以用分離原理設計全局最優控制系統的一類問題。對於離散時間的情況,受控對象用如下線性差分方程來描述:
性能指標取為二次型的形式:
式中上標T表示向量的轉置,裝置噪聲
w(
t)和量測噪聲
v(
t)為高斯隨機過程。並且假定控制
u(
t)可依據
t時刻及以前的觀測數據
y(
t),
y(
t-1),…來確定。按照分離原理,隨機最優控制的結構具有圖中的形式。它由狀態估值器給出狀態
x 的估計值憫,再由憫 隨機控制理論
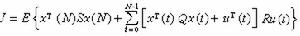 方程
方程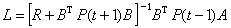 隨機控制理論
隨機控制理論按線性狀態反饋律u=-L憫確定控制量u。這裡狀態反饋矩陣L是在不考慮隨機干擾w(t)和v(t)時的確定性最優控制問題的解:
而P(t)滿足黎卡提方程
和邊界條件
P(
N)=
s。狀態估計一般用卡爾曼濾波器來實現。整個控制結構可用微型或小型計算機來實現。
 方程
方程
 隨機微分方程
隨機微分方程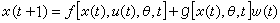 隨機差分方程
隨機差分方程
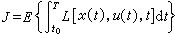 統計平均
統計平均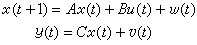 線性差分方程
線性差分方程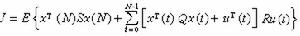 方程
方程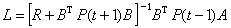 隨機控制理論
隨機控制理論 方程
方程

