H∞最優控制,簡而言之,就是用H∞範數作為目標函式的度量邊行最佳化設計。H∞範數是定義在Hardy空間 上的範數,在H∞控制理論中是指在S右半平面上解析的有理函式陣的最大奇異值。
基本介紹
- 中文名:H∞最優控制
- 外文名:H-infinity optimal control
- 學科:控制科學與工程
- 創始人:Zame
- 時間:1981年
- 分類:最優控制和次優控制
基本概念

H∞控制問題描述
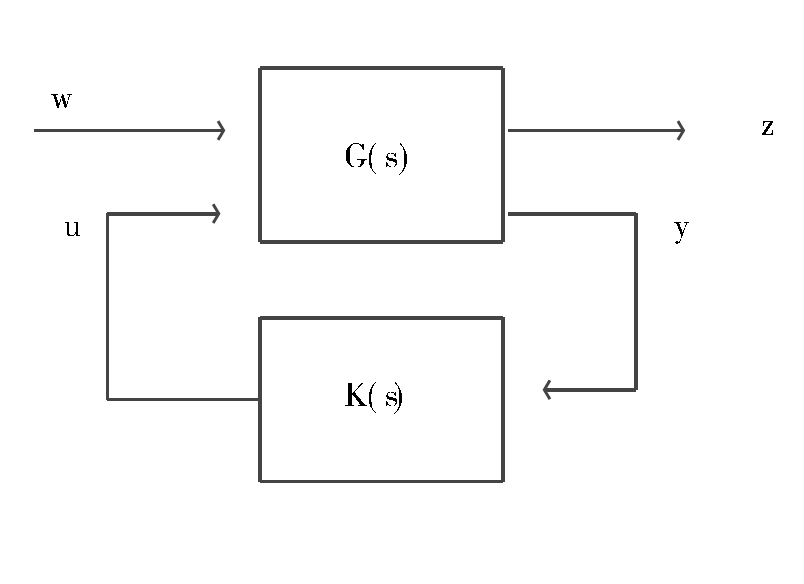
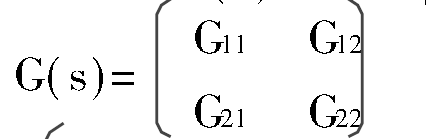
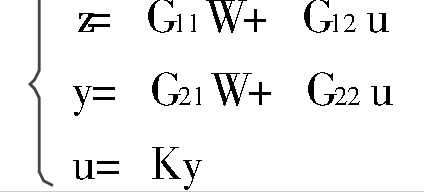
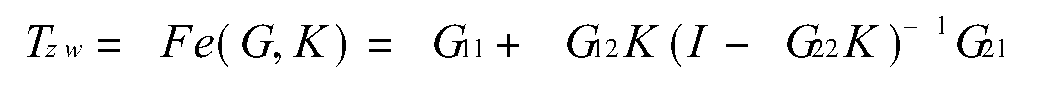
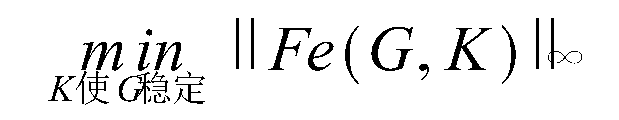
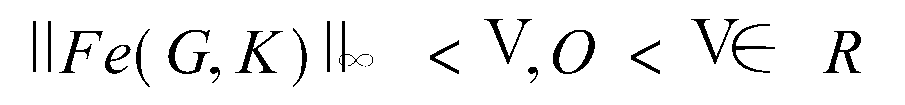
H∞最優控制方法的套用
魯棒穩定問題
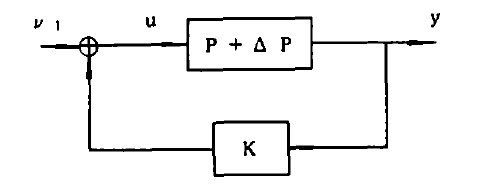
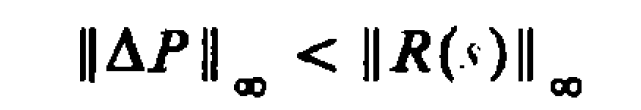
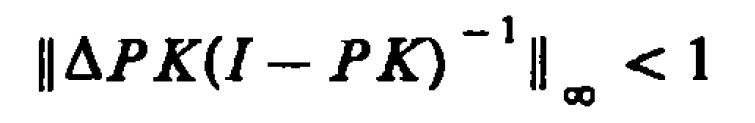
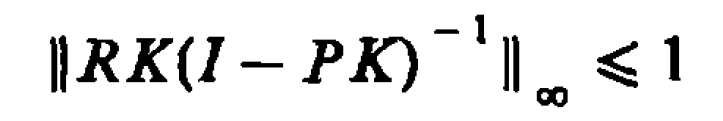
二次穩定問題
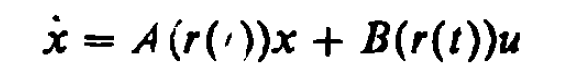
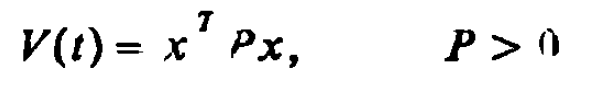
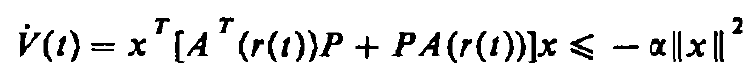
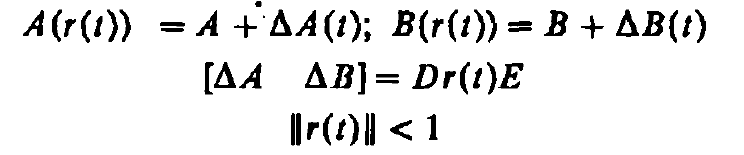
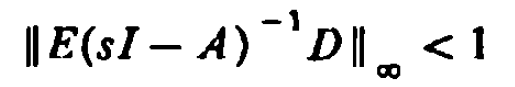
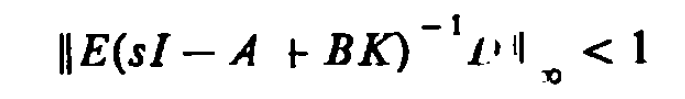
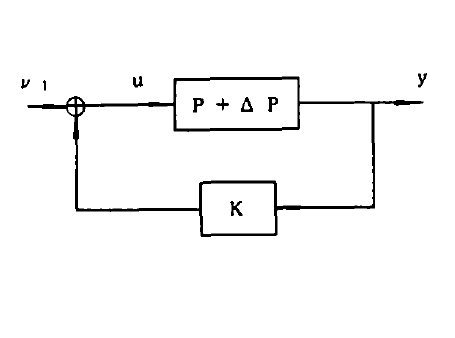
H∞最優控制,簡而言之,就是用H∞範數作為目標函式的度量邊行最佳化設計。H∞範數是定義在Hardy空間 上的範數,在H∞控制理論中是指在S右半平面上解析的有理函式陣的最大奇異值。


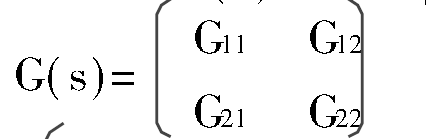
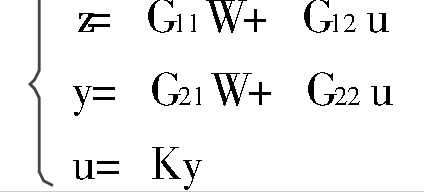
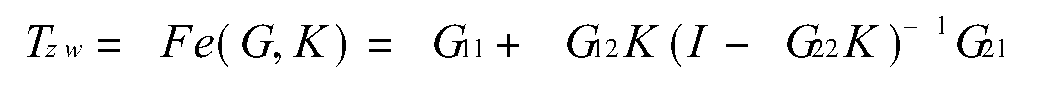
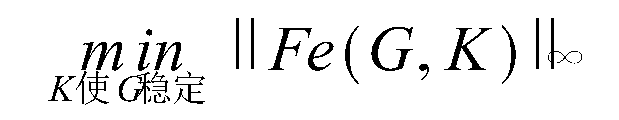
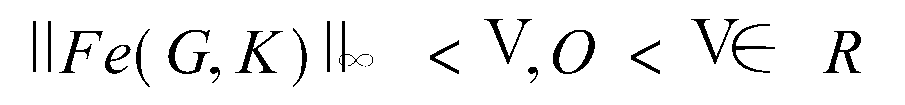

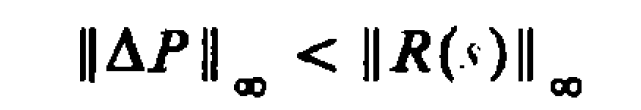
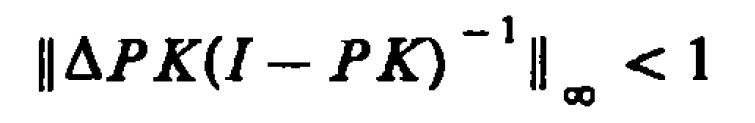
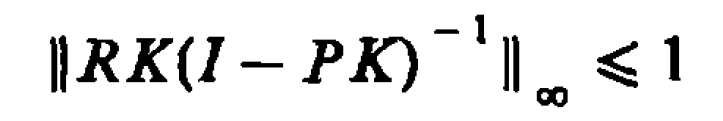
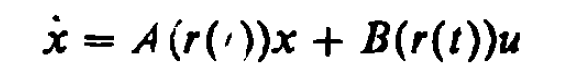
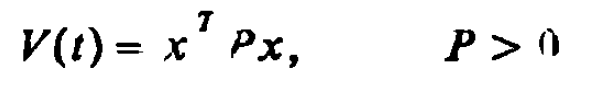
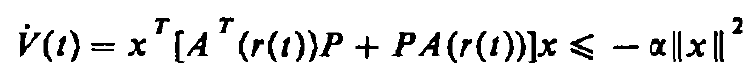
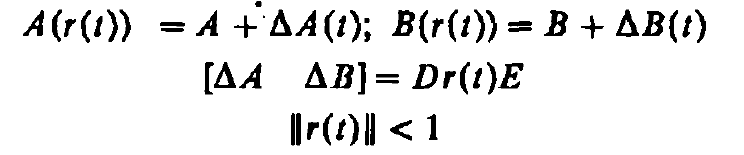
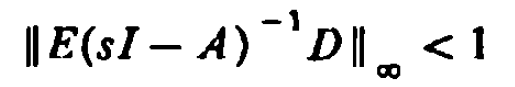
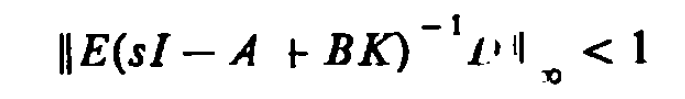
H∞最優控制,簡而言之,就是用H∞範數作為目標函式的度量邊行最佳化設計。H∞範數是定義在Hardy空間 上的範數,在H∞控制理論中是指在S右半平面上解析的有理函式...
H∞控制方法始於1981年,Zame把SISO線性反饋系統的靈敏度問題看作是H∞最小範數問題,並涉及了古典控制理論的一些基本問題,立即引起了人們的極大注意。目前主要有...
其最優擾動抑制問題敘述為:對所有範數在某一定界限的擾動,系統都能將其抑制到最小。數學上可採用H∞空間來處理,故而這種方法稱為H∞最優控制。...
H∞控制方法始於1981年,Zame把SISO線性反饋系統的靈敏度問題看作是H∞最小範數問題,它比其它方法更為直接。H∞控制的表示很簡單,但求解過程卻十分複雜。目前主要...
魯棒最優控制是在60 年代發展起來的一種設計方法, 它以狀態空間描述的線性系統為對象, 以狀態變數和控制變數的二次型函式的積分為目標, 得到的反饋控制律可以實現...
最優控制理論(optimal control theory),是現代控制理論的一個主要分支,著重於研究使控制系統的性能指標實現最最佳化的基本條件和綜合方法。 最優控制理論是研究和解決...
《最優控制理論及其套用》是2010年大連理工大學出版社出版的圖書,作者是錢偉懿。...... 7.3 非線性系統的H∞控制7.3.1 仿射非線性系統的L2-增益與次優控制...
魯棒最優控制理論與套用一書闡述了不確定性系統魯棒穩定和魯棒性能這一魯棒控制的關鍵問題,介紹了魯棒最優控制的基本概念、理論和方法,以及其工程套用。...
11.7.3H∞最優控制11.7.4線性離散時間系統H∞自適應控制11.8預測控制11.8.1預測控制的一般描述11.8.2廣義預測控制方法11.8.3MIMO系統的廣義預測控制方法...
《結構隨機跳變系統最優控制理論》是關於結構隨機跳變系統最優控制理論與套用的一本著作。書中重點介紹了近十幾年國內外學者在此領域的最新研究成果,詳細討論了...
《變分法和最優控制論(英文版)》是一部講述變數微積分和最佳化控制理論的嚴謹、詳盡、自成體系的工程類、套用數學、及相關科目的研究生教程。書中的內容從變數微...
第10章 離散系統分析與控制10.1 線性連續系統的精細離散化10.2 離散系統線性二次最優控制10.3 離散系統的H∞控制參考文獻第11章 時滯系統最優控制...
近世代數、微分幾何、隨機過程、泛函分析等必要的數學工具; 第二部分介紹最優控制、H∞-控制、非線性控制、自適應估計與控制、分布參數系統控制、及離散事件動態...
參考文獻第4章狀態反饋 H ∞ 最優控制4.1簡介4.2信號和系統範數4.2.1功率信號4.2.2系統範數4.2.3系統範數的計算4.2.4適定性和穩定性4.3頻域穩定性和性能指標...
主要的魯棒控制理論有:(1)Kharitonov區間理論;(2)H∞控制理論;(3)結構奇異值理論(μ理論)等等。被控對象的不確定性對各種控制方法都提出了魯棒性的要求,有各種...
6.5.2 標準H∞控制問題小結習題第7章 泛函最佳化與最優控制7.1 凸集與凸函式7.1.1 凸集的基本概念7.1.2 凸集分離定理及其套用...
11.7.3H∞最優控制11.7.4線性離散時間系統H∞自適應控制11.8預測控制11.8.1預測控制的一般描述11.8.2廣義預測控制方法11.8.3MIMO系統的廣義預測控制方法...
最優控制與最佳化,魯棒控制與H∞控制,自適應控制與學習控制,變結構控制,神經網路,模糊系統與模糊控制,模式識別,控制設計方法,遺傳算法與演化計算,運動控制,智慧型機器人...
最優控制、最佳化方法、魯棒控制、H∞控制、預測控制、過程控制、隨機控制、自適應控制、穩定性分析、分布參數系統、DEDS與CIMS、複雜系統、模糊系統與控制、神經網路、...
第5章介紹了三相變流器的電流控制,包括基於線性二次型最優電流控制和神經網路...5.4.3 H∞電流控制……136 5.5 三相變流器神經網路電流控制技術研究……138 ...
最優控制與最佳化,魯棒控制與H∞控制,自適應控制與學習控制,變結構控制,神經網路,模糊系統與模糊控制,模式識別,控制設計方法,遺傳算法與演化計算,運動控制,智慧型機器人...
全書的內容分為兩部分:第一部分結合控制理論討論線性系統、近世代數、微分幾何、隨機過程、泛函分析等必要的數學工具:第二部分介紹最優控制、H∞控制、非線性控制、...
分散式控制系統,隨機系統,信息處理系統,穩定性與鎮定,故障診斷,建模、辨識與信號處理,通訊網路系統,最優控制與最佳化,CIMS與製造系統,魯棒控制與H∞控制,交通系統,自...
第6章自適應控制系統6 1自適應控制系統的基本概念6 2模型參考自適應控制6 3自校正自適應控制6 4 2H∞魯棒控制理論第7章最優估計...
馬廣富,分別於1983年、1987年、1993年在哈爾濱工業大學自動控制專業,自動控制理論...2.馬廣富,楊志紅,基於有限維YOULA參數化的多目標H2/H∞最優控制,電機與控制...
穩定性概念與基本理論、能穩性理論和特徵多項式配置、局部能達性與局部能觀性的基本概念和理論、觀測器與補償器設計、H∞控制與濾波,以及最優控制與Kalman濾波等...
褚健1989年回國工作以來一直從事自動控制理論前沿學科的研究,提出了時滯系統狀態空間建模方法、多滯後魯棒最優控制策略和時變時滯系統的H∞最佳化控制方法,並利用這些理論...
3.《結構抗震H2/H∞最佳化控制與仿真》,東北大學出版社,2006。4.廣義系統的H2最優控制,自動化學報, 2002. (EI 檢索)。5.廣義系統的H2 次優控制問題的一個...
