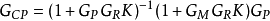簡介
魯棒最優控制是在60年代發展起來的一種設計方法,它以狀態空間描述的線性系統為對象,以狀態變數和控制變數的二次型函式的積分為目標,得到的反饋控制律可以實現最優控制。由於這種方法計算容易,控制效果明顯,所以套用範圍十分廣泛。近年來,H∞控制理論得到了很大發展,理論也不斷得到完善,研究的對象主要針對含有建模不確定性等因素造成參數攝動的系統,設計得到的控制器具有魯棒性好的特點,套用前景良好。
發展歷史
控制科學從產生、發展到輝煌,幾乎貫穿了整個20世紀。對它的研究從一開始就表現出與研究其他自然科學(例如物理學)不同的特點。少受干擾與純粹化是自然科學中研究基本原理的準則。控制科學由於其目的是針對現實解決問題的,因此從它一產生起就必須不斷地考慮干擾和非純粹化的影響,而且,在不同階段不同條件下這種考慮有其不同表現。
控制科學中最重要的一個概念就是反饋,而反饋的最主要之點就在於考慮了實際系統中存在的不確定性。人們發現,當反饋不再限於常數增益而是動態系統時,反饋在閉環系統動力學中十分重要。在一定程度上它可使閉環系統具有合適的動態特徵而不受開環所可能產生的攝動影響。這一點能奏效的原因之一是系統簡單。
隨著控制系統套用範圍的擴大,對象的日益複雜,系統與環境均充滿不確定性以及更為嚴格的控制要求,使我們正面對一個系統複雜程度日益增大和控制要求日益提高的充滿挑戰的時代。而控制系統複雜性中不確定性是最重要的一個因素。大量數學工具從套用角度引入控制研究和計算機技術的飛速發展為迎接這個挑戰創造了條件。這就是20世紀80年代出現的魯棒控制飛速發展的前提。
G.Zames在1981年發表的著名論文,可以看成是現代
魯棒控制特別是H∞控制的先驅。它以最優敏感性,即干擾在輸出上影響最小作為H∞控制的基本提法。這實際上是Wiener—Hopf理論和二次型最優控制的發展。但隨後的研究發現,這種H∞最優控制的求解實際上可以解決一系列魯棒控制問題。這表明魯棒控制與最優控制具有某種深刻聯繫。
H∞控制中一個具有里程碑性質的結果是J.C.Doyle等四人的著名文章。他們將H∞問題的求解歸結為求解兩個Riccati方程,從而溝通了二次型最優控制與H∞控制的本質聯繫。如同絕對穩定性問題的研究中Popov頻域方法與Lyapunov函式的時域方法得到溝通時出現的學術繁榮場面一樣,這一新的突破性的聯繫就使得H∞的研究獲得了新的推動力,使在理論上和計算上均取得了極大的發展,從而使線性H∞控制的研究在幾年裡就取得成功並達到基本完善。
隨後,周克敏博士所著《RobustandOptimalControl》,正是適應這個形勢需要,及時地對線性魯棒與最優控制,特別是對H∞控制進行了總結提煉並系統化,使其成為這個領域最早的高水平的理論著作。
魯棒性(Robustness)
無論是對於何種形式的預測控制算法,魯棒性研究一直是其理論研究中的薄弱環節。實際工業過程存在於不確定性環境,總會受到預先未知的各種不確定性的影響;模型和被控對象之間也不可避免地存在著失配。基於模型設計的最優控制律套用於實際對象可能導致系統性能變差,因此研究MPC魯棒性是十分必要且有實際意義的。總的來說,MPC魯棒性問題的研究分魯棒分析和魯棒綜合兩個方面。
MPC魯棒性分析
Garcia和Morari於80年代初提出在IMC框架下研究MPC性能,並簡單分析了MPC系統的魯棒性,推導了預測控制在內模控制結構下的定量表達,然後由模型和對象之間的失配來分析魯棒性,其優點是可以定量地研究設計參數與系統魯棒性間的關係,但較局限。在上述基礎上,又研究了一類MPC系統在模型增益失配和時滯失配時的魯棒性,給出了增益和時滯的允許失配範圍,以及失配度變化趨勢和系統魯棒穩定性的關係,但所得定理只是充分的,且僅針對這一類系統。隨後,以對象到閉環系統特徵多項式的係數映射為基礎,分析了CARIMA模型中噪聲濾波器T對於閉環系統魯棒性的影響,並通過比較得出
GPC中
噪聲濾波器T作為設計參數時,其地位實際上相當於
DMC中的校正參數,它們都對模型失配時的閉環系統魯棒性產生很大影響。
MPC魯棒綜合
魯棒綜合問題是建立在被控對象模型不確定性描述基礎上的。大多數魯棒MPC設計都基於min-max描述,具有H∞控制的思想,即將MPC的線上min最佳化問題變為min-max最佳化,求解控制律使在不確定性最壞情況(worstcase)下的目標函式值最小。根據目標函式和不確定性描述的不同,可將魯棒MPC設計分為如下三類:
1)基於不確定FIR模型的min-max設計。
2)基於LMI的MPC。
3)滾動時域H∞控制。
魯棒最優控制器
結構及原理
魯棒控制理論保證了系統在參數攝動和外加干擾情況下具有閉環穩定性,但是對於隨動系統而言,良好的跟隨特性是必須的要求,為了達到滿意的效果,得到如圖所示的控制結構。
 魯棒最優控制器採用的結構
魯棒最優控制器採用的結構在圖所示結構中,P為對象的實際模型,設P0s為P的數學模型,即標稱對象,P0為P的標稱對象P0s與控制器K2形成的閉環,d為外加干擾,K1、K2、K3為控制器,輸入為r,輸出為y0。
對上述控制結構的解釋如下:由於對象的實際模型可能存在一定的參數攝動,並且對象本身可能受到外部干擾,引入魯棒控制器K2就是為了增強系統的魯棒性,抑制干擾,降低系統對對象參數攝動的敏感度;K1為最優控制器,它根據P0進行設計,目的是滿足系統的跟隨特性;控制器K3的作用是消除實際系統輸出y與標稱系統輸出y0之間的誤差,當P=P0s,即實際對象與標稱對象一致的時候,有y=y0;當P≠P0s時,y與y0就不相同,可以通過控制器K3的調節使得y與y0達到一致。
控制器設計
最優控制器K1的設計由如下定理給出。設系統輸出的期望值為y0,二次型性能指標為
則最優控制器為
控制器K3的參數可以通過仿真得到,調節的標準是使得實際對象與標稱對象輸出之間的誤差衰減具有良好的動態特性。
機器人的魯棒最優控制結構
機器人單通道速度控制系統的魯棒最優控制結構如圖所示。
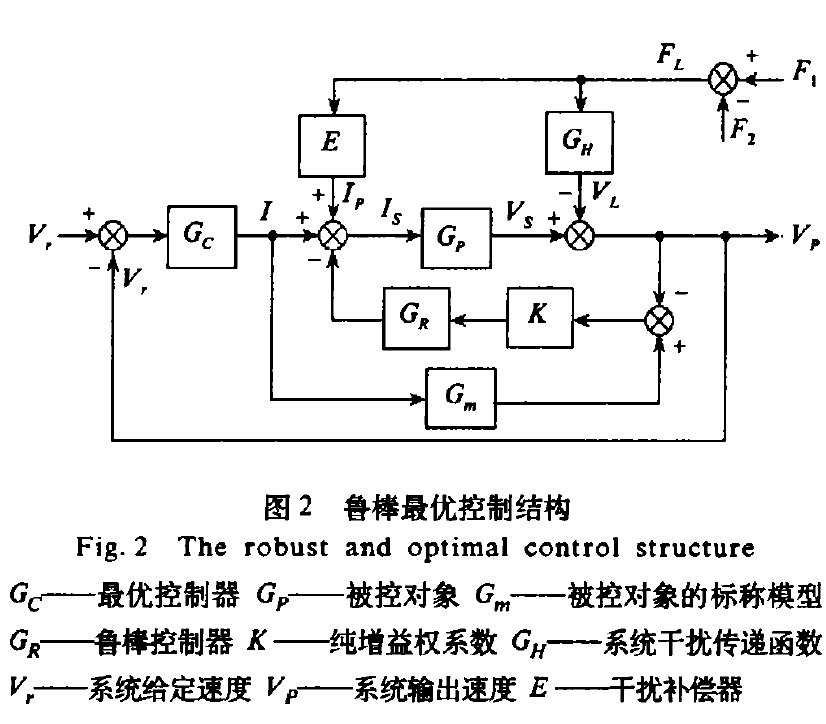 魯棒最優控制結構
魯棒最優控制結構由於並在線上器人各通道間存在嚴重的非線性藕合干擾,使實際系統設計時的魯棒控制只能削弱或抑制干擾的影響,所以,為提高機器人的操作精度,可同時設計干擾補償器,對於單一通道,藕合作用集中表現為負載及干擾的影響,即表現為負載壓力的變化FL,可選擇負載壓力FL為觀測量,設定補償器E,通過合理設計即可消除負載及干擾的影響。
在系統中,可通過檢測油缸無桿腔的壓力F1和有桿腔的壓力F2來間接觀測負載壓力。
由圖,Gp,Gm,GR,K實際構成了一個典型的IMC結構。因此,系統對於模型的不確定性和干擾均具有強魯棒性。採用魯棒控制器後。被控對象的等效傳遞函式為
因當K充分大時,Gcp≈Gm,故最優魯棒控制器Gc可按被控對象標稱模型Gm以系統具有最優跟蹤特性為目標進行設計,而魯棒控制器GR可按系統輸出干擾影響最小為目標進行設計。兩種控制器可分別獨立進行設計。
 魯棒最優控制器採用的結構
魯棒最優控制器採用的結構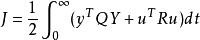



 魯棒最優控制結構
魯棒最優控制結構