非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
基本介紹
- 中文名:非分歧擴張
- 外文名:unramified extension
- 領域:數學
- 學科:域論
- 性質:一類重要的域擴張
- 相對概念:分歧擴張
概念







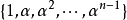
非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F。此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。







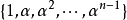
非分歧擴張(unramified extension)是一類重要的域擴張。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常...
全分歧擴張(totally ramified extension)是一類有限賦值域擴張,它是與非分歧擴張相反的概念。賦值域(F,B)的一個有限擴張(K,C),若分歧指數e(C|F)=[K∶F],...
馴分歧擴張(tamely ramified extension)一類包括非分歧擴張在內的代數擴張.設(K,C)是賦值域(F,B)的一個代數擴張,F和I', K和。分別是賦值環B,C的剩餘域和...
分歧指數(ramification index)是在域擴張時,素除子延拓或素理想分解的指數。域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴...
分歧定理(ramification theorem)類域論中判定素理想分歧的定理.若K/k是H的類域,這裡H是k的伊代爾群Jk的含k‘的子群.則k的任一素除子在K非分歧若且唯若Uz....
順分歧(tamely ramified)一種較簡單的分歧情形,包括非分歧情形.設Q為域E的離散素除子,P為其在子域F'上的限制.若剩餘類域擴張E/F可分,且F,的特徵p為零或...
否則就稱為非分歧。如果OK中所有的素理想在L中都是非分歧的,L就稱為K 的一個非分歧擴張。判別式與差積是刻畫分歧的兩個重要概念。令Tr表示有限擴張L到K 的...
希爾伯特類域(Hilbert class field)亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論...
希爾伯特類域亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論。數域k的希爾伯特類域...
5.2 非分歧擴張5.3 完全分歧和順分歧5.4 慣性群與分歧群5.5 整體域與局部域5.6 差分5.7 差分與分歧5.8 判別式第六章 整體域:類數與單位...
他給出了關於定義在有限域上的多元函式域的非分歧阿貝爾擴張的定理。在數論中,他推廣了關於丟番圖方程整數解個數的西格爾(Siegel)定理。...
構成的全部非零理想,從而也是主理想環。/是(P)元有限域,稱為的剩餘類域,...此外,局部數域也有判別式,差積等概念和希爾伯特分歧理論,與代數數域擴張的情形...
P類域(p-class field )一種阿貝爾擴張.數域k的p類域K }"即為k的最大非分歧阿貝爾p擴張(p擴張即伽羅瓦群元素的階均為p的冪的擴張.這裡p均指有理素數)....
