類域塔問題(problem of class field tower)是關於是否可以有無限長的希爾伯特類域鏈的問題。設有域擴張序列K0K1K2…,其中Ki是Ki-1的希爾伯特類域,這樣的序列稱為類域塔。
基本介紹
- 中文名:類域塔問題
- 外文名:problem of class field tower
- 領域:數學
- 學科:類域論
- 性質:希爾伯特類域鏈的問題
- 證明:戈羅德
概念,希爾伯特類域,類域論,域擴張,
概念
類域塔問題(problem of class field tower)是關於是否可以有無限長的希爾伯特類域鏈的問題。設有域擴張序列K0K1K2…,其中Ki是Ki-1的希爾伯特類域,這樣的序列稱為類域塔。問題是類域塔是否可能無限擴展下去?這一問題有很長的歷史,事實上在證明主理想定理時,要用到兩層的類域塔。直到1964年,由戈羅德(Golod)與沙發列維奇(Shafarevich)給出肯定的回答,他們證明:當
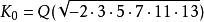
希爾伯特類域
希爾伯特類域亦稱最大非分歧阿貝爾擴張。一種重要的類域。最早由希爾伯特(Hilbert,D.)於1898年至1899年猜出,後來發展為系統而一般的類域論。數域k的希爾伯特類域K有下列性質:
1.伽羅瓦群G(K/k)與k的理想類群同構。
2.k的素理想p在K完全分裂若且唯若p為主理想。
3.K是k的最大非分歧(對有限和無限素除子)阿貝爾擴張。
4.k的任一理想到K均為主理想。
類域論
類域論是代數數論的重要理論之一。它深刻地刻畫了(相對)阿貝爾擴張。基本定理如下:若K/k為數域的有限阿貝爾擴張,伽羅瓦群為G=G(K/k),則存在k的模f(稱為K/k的導子,是k的一個除子),使得對k的任意的模m,由f|m得出G同構於m射線類群I(m)/PmN(m),式中I(m)為與m互素的k的理想集,N(m)為與m互素的K的理想到k的范全體,Pm為模m餘1的α∈k生成的主理想集。且k的素除子v在K分歧若且唯若v|f;k的與m互素的素理想p在K完全分裂若且唯若p∈PmN(m);反之,對k的任一模m及I(m)的任一含Pm子群H,總存在惟一阿貝爾擴張K/k,使得H=kPmN(m)且上述事實均成立。特別地,G(K/k)I(m)/H.更經常的是用伊代爾語言敘述類域論的定理.基本定理:若K/k為數域的有限阿貝爾擴張,則伽羅瓦群G(K/k)同構於Jk/kNJk,式中Jk為k的伊代爾群,NJK為K的伊代爾群到k的范.上述群的同構由阿廷映射給出。由此可得出,數域k的諸有限阿貝爾擴張K/k與Jk的含k諸開子群H之間一一對應,即K對應於H=kNJK,稱為H的類域,G(K/k)Jk/H;這一對應是這兩個格(對於複合(或積及交))的反向(包含關係)格同構。類域論有系統的定理和套用,有多種不同的表述方式。對於局部域的阿貝爾擴張有類似的定理(局部類域論),對於有限域上的單變數函式域也有類似的定理。
域擴張
域擴張是域論的基本概念之一。若域K包含域F作為它的子域,則稱K是F的一個擴張(或擴域),F稱為基域,常記為K/F.此時,K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質,是域論研究的一個基本內容。
若域E是F的擴域,K是E的擴域,則稱E是域擴張K/F的中間域。若K/F是域擴張,S是K的子集,且F(S)是K的含F與S的最小子域,稱F(S)為F添加S的擴域。當S={α1,α2,…,αn}是有限集合時,F(α1,α2,…,αn)稱為添加α1,α2,…,αn於F的有限生成擴域(或者F上的有限生成擴張)。它由一切形如f(α1,α2,…,αn)/g(α1,α2,…,αn)的元組成,其中α1,α2,…,αn∈S,f,g是F上的n元多項式且g(α1,α2,…,αn)≠0。
由於這個原因,當F(α1,α2,…,αn)關於F的超越次數≥1時,F(α1,α2,…,αn)也稱為F上的代數函式域。當S={α}時,稱F(α)為F的單擴張域,也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是,擴域K與基域間存在有限箇中間域。這是施泰尼茨(Steinitz,E.)證明的。
