基本介紹
基本介紹
無窮公理
並集公理


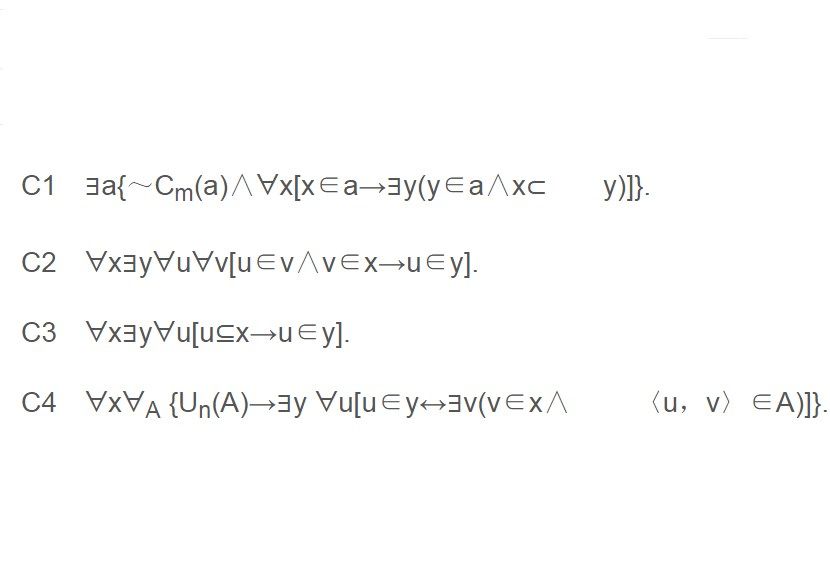


集合存在性公理(existence axiom of set)是GB系統的集合論公理,指GB系統中的第3組(即C組)公理,共有4條,包括無窮公理,並集公理,冪集公理,和替換公理。基本介紹集合存在性公理是GB系統的集合論公...
存在性公理 存在性公理(axiom of existence)集合論的一條重要公理.該公理斷言:至少存在一個集合.要討論集合,自然首先要假定集合存在.該公理在後來的ZF系統中被刪去,因為在ZF系統中的無窮公理就是存在性公理.
(ZF2)空集合存在公理:即存在一集合s,它沒有元素。(ZF3)無序對公理:也就是說,任給兩個集合x、y,存在第三個集合z,而w∈z若且唯若w=x或者w=y。註:z = {x, y}, 就是說,如 w∈z, 則 w=x 或 w=y。又...
(5)冪集公理(子集之集公理):對任意集合X,存在集合P(X),它的元素恰好就是X的一切子集。也就是說:存在以已知集合的一切子集為元素的集合。(6):無窮性公理存在歸納集。(存在一個集合,空集是其元素,且對其任意元素x,xx∪{...
並集公理可以得出包含公理:對任意兩集 X 與 Y,存在同時以 X,Y 為子集的集合。簡介 引入 並集公理(axiom of inclusion)是集合論的一條重要公理。由策梅洛 (Zermelo,E.F.F.) 於 1908 年提出。該公理斷言:對任何集合 X,存在...
GB公理集合論系統(GB axiomatic set theory system)一種近代公理集合論系統.該系統是由美籍匈牙利數學家馮·諾伊曼(von Neumann, J.)於 1920年首先給出的,德國學者貝爾奈斯(Bernays, P.)於1937年以後的一系列重要論文中又進一步發展了...
在後來的著作中,皮亞諾對這一算術系統作了修改,去除了關於“相等”的四條公理,並且以0取代1作為基本概念,構造了沿用的皮亞諾算術公理系統。定義 目的是定義自然數集合,首先需要承認的是集合具有的一些運算性質,例如:a=b時a,b...
關於實數的完備性,注意完備性公理中出現的“完備性”,以及關於實數完備性最常見的描述中,所謂“完備性”是對集合(有序域)性質的一種描述。此外還有其它完備性,例如作為公理系統所確定的數學對象是否唯一(同構意義上)也稱為完備性...
所有有理數的集合Q就是阿基米德有序域,但它不滿足完備性公理。根據域公理,可以定義實數的減法和除法,並證明四則運算的所有性質。序公理的1與2表明關係“>”是R的全序。用域公理和序公理可以定義正數、負數、不等式、絕對值,並證明...
這裡對被數學家們稱為“直觀的”或“樸素的”集合論進行一個簡短而基本的介紹;更詳細的分析可見樸素集合論。對集合進行嚴格的公理推導可見公理化集合論。集合(或簡稱集)是基本的數學概念,它是集合論的研究對象。最簡單的說法,即是...
羅素公理體系與羅素悖論 羅素悖論產生的原因,是把真類當成集合。可以說,羅素公理體系在兩方面避免羅素悖論:第一,不存在包含自身的集合(包含自身的類是真類)。第二,“所有”集合的總體不是集合!而是一個真類。因為“所有”一詞...
公理集合論ZFC中的公理不具有獨立性,即並非都是不可缺少的.有了子集公理實際上我們可以證明空集公理.因為,根據定理可知,集合是存在的,那么我們可以任意取定一個集合A,然後使用x≠x作為性質ψ(x),那么根據子集公理有:∃Bᗄx...
選擇公理 選擇公理(英語:Axiom ofChoice,縮寫AC)是數學中的一條集合論公理。這條公理聲明,對所有非空指標集族,總存在一個索引族,對每一個 ,均有 。選擇公理最早於1904年,由恩斯特·策梅洛為證明良序定理而公式化完成。非...
然而並沒有任何跡象表明可以將可構造性公理作為集合論基本假設加到ZFC公理系統中,相反地,隨著大基數理論的研究,人們發現某些大基數的存在性與可構造性公理相悖,如假設可測基數存在,則可以證明存在不可構造的集合,而某些大基數的存在...
更加明確地說,在樣本集合之外已經不存在基本事件了。 這在一些錯誤的機率計算中經常被小看;如果你不能準確地定義整個樣本集合,那么任意子集的機率也不可能被定義。第三公理 任意兩兩不相交事件E₁, E₂, ...的可數序列滿足P(E...
所以,概括原則是一條集合存在性公理(公理模式)。在德國數學家康托爾(Cantor,G.(F.P.))的早期工作中,概括原則只是隱蔽地被使用著,後來德國數學家、數理邏輯學家弗雷格(Frege,(F.L.)G.)公開地採用這一公理模式。對於概括原則...
最後,素理想定理也存在於其他(非序理論的)抽象代數中。比如,環的 MIT 蘊涵了選擇公理。這種情況需要把序理論的術語"濾子"替代為其他概念 -- 對於環"乘法閉合子集"是合適的。超濾子引理 在集合 X上的濾子是 X 的非空子集的蒐集...
在集合論範疇.為了排除集合論中的悖論,促使了現代公理集合論的誕生,其中最著名的有兩個,即是由Bernays與Gödel建立的BG公理集合認最完善的一個系統。這些系統有一個共同點,即是在保留概括原則的“合理因素”的前提下。對造集的...
不存在以自身為元素的集合 反證,假設有一個集合A,使得A是自身的一個元素,即 。這時,根據配對公理,可以構造出B= {A},B也是一個集合。由於B中只有一個元素A,根據正則公理,我們得到 。但是根據我們的假定有 及 ,所以 。這...
