基本介紹
- 中文名:冪集公理
- 外文名:axiom of power set
- 所屬學科:離散數學
- 相關概念:冪集、外延公理、有限集合等
基本介紹
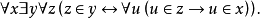
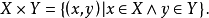
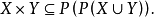

相關性質定理
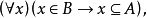
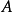
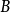
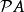
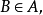
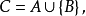
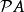
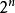

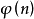
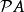
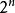
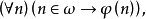
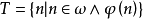

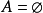
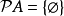
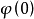
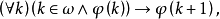
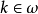
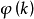
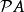
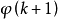
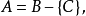
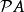
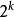
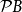
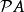
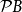
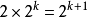
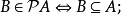
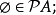
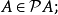
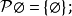
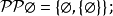
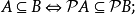
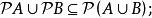
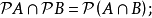

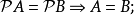
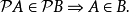
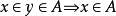
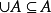
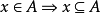
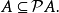
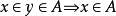
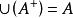
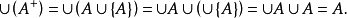

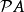
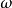

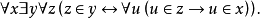
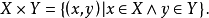
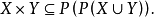

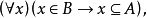
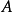
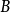
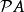
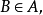
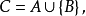
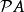
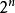

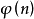
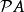
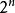
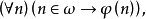
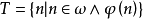

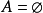
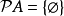
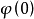
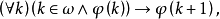
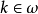
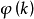
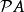
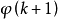
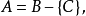
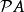
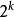
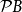
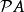
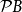
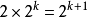
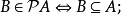
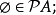
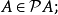
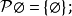
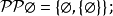
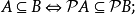
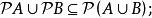
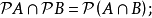

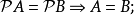
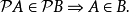
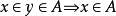
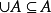
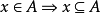
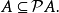
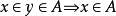
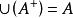
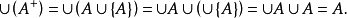

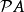
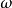
在數學中,冪集公理是公理化集合論的 Zermelo-Fraenkel 公理中的一個。這個公理說明:“對於任何一個集合A,存在著一個集合B,它的元恰是A的各個子集。...
集合存在性公理(existence axiom of set)是GB系統的集合論公理,指GB系統中的第3組(即C組)公理,共有4條,包括無窮公理,並集公理,冪集公理,和替換公理。...
所謂冪集(Power Set), 就是原集合中所有的子集(包括全集和空集)構成的集族。可數集是最小的無限集; 它的冪集和實數集一一對應(也稱同勢),是不可數集。 ...
初等集公理是集合論的一條公理,策梅洛(E.F.F.Zermelo)於1908年提出集合論公理體系時,其中有一公理稱為初等集公理,該公理斷言:存在空集,它不含任何元素;如果a...
這個系統中只有一個非邏輯二元關係符號“∈”,非邏輯公理有:外延公理、空集公理、無序對公理、並集公理、冪集公理、無窮公理、分離公理模式、替換公理模式、正則...
在集合論中,有了外延性公理、空集公理、對集公理、子集公理模式、並集公理、冪集公理和無窮性公理這7條公理,就可以定義自然數、實數等數學對象,但仍有很多重要的...
1.類外延性公理2.外延性公理3.類概括公理(模式)4.配對公理5.大小限制公理6.並集公理7.冪集公理8.無窮公理9.類基礎(正規)公理...
(3)並集公理:任給一個集合X,都有一個恰好由X的元素的元素之全體所組成的集合 ,即(4)冪集公理:任給一個集合X,都有一個恰好由它的子集合的全體組成的集合P...
他在1908年建立了第一個集合論公理系統,給出了外延、空集合、並集合、冪集合、分離、無窮與選擇等公理,A.A.弗倫克爾和A.T.斯科朗又作了改進,增加了替換公理,...
對造集的任意性加以適當限制。ZFC系統包括了處延、空集、配對、並集、冪集、子集(即劃分)、無窮、選擇、替換、正則等10條非邏輯公理。Zermelo於1908年建立了他...
} an,使A={x:}p}x,al,aZ,...}a )}.由於在 OD中可以定義一種良序關係,因此AC在OD中成立,並且在其中可以證明無序對公理、並集公理、冪集公理等但在ZF...
他在1908年建立了第一個集合論公理系統,給出了外延、空集合、並集合、冪集合、分離、無窮與選擇等公理,A.A.弗倫克爾和A.T.斯科朗又作了改進,增加了替換公理,...
可構造集全域(u niverse of constructible sets)是 一種可構造集模型。美籍奧地利數學家哥德爾 (Godel , K.)用於證明連續統假設與選擇公理的相容性所構造的ZF...
基數亦稱勢。公理集合論的基本概念之一。是度量集合大小的量。在德國數學家康托爾(Cantor,G.(F.P.))之前,無窮只是一個很模糊的概念,人們無法區分兩個無窮集...
它的非邏輯公理有:外延公理、空集公理、無序對公理、並集公理、冪集公理、替換公理模式、正則公理。如果另加選擇公理(AC),則所得到的公理系統簡記為ZFC。...
