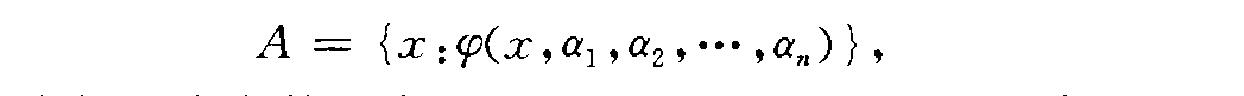
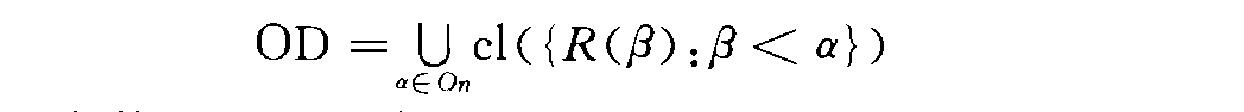
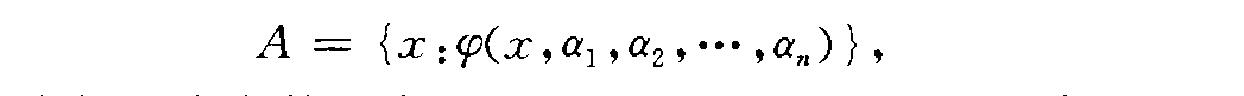
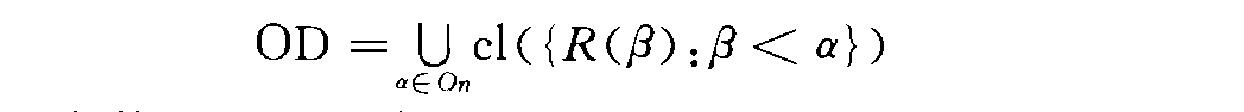
簡介 序數可定義集(ordinal-definable set)簡稱 OD一種特殊的集合.能在集合論語言中由有限個序數所定義的集合稱為序數可定義集.設A為一個集合,若存在公式筍及...
集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。...
可構造序數(constructive ordinal)是一種特殊的序數。α為可構造序數,是指存在一個記號系統S,使得S中有α的記號。可構造序數都是可數序數,可構造序數的全體構成...
而序數就可定義作為同構的良序集的代表。依此,可以定義序數的運算。例如,序數的加法可以定義如下:若α,β為序數,γ為極限序數。即用關於α的超限歸納原理來定義...
可構造序數是一種特殊的序數。α為可構造序數,是指存在一個記號系統S,使得S中有α的記號。可構造序數都是可數序數,可構造序數的全體構成序數的一個前節,並且可...
任一序數上都可定義序拓撲(即以開區間組成的集族為基的拓撲),故可視為一個拓撲空間。視ω1為拓撲空間時,通常記為 [0,ω1) ,以強調其為所有小於 ω1的...
在序數的廣泛實際使用的驅動下,已經定義了許多特殊類型的序數集合,其中一些已經成為它們自己的數學領域。此外,序數理論不限於各種類型的排序關係,而是考慮它們之間的...
序數是集合論基本概念之一。是“第一”、“第二”等表示次序的數在概念上的推廣。康托爾原來把序數定義為良序集a的序型ā,作為所有與a序同構的集的共同特徵,...
序數是集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。序數類閉...
後三種定義沒有康托爾原定義的缺點。序數有三種,第一種是0;第二種是後繼序數α′=α∪{α};其他序數屬第三種,稱為極限序數。對任何良序集A,有且僅有一個...
序數算術編輯 鎖定 討論 本詞條由“科普中國”科學百科詞條編寫與套用工作項目 審核。序數算術包括序數加法、序數乘法、序數方冪、序數除法。...
原子序數定義 編輯 原子序數是一個原子核內質子的數量。人們按照核電荷數由小到大的順序給元素編號,這種編號叫原子序數。元素的原子序數在數值上等於該元素原子的核...
序數的無界子集(unbounded subset of ordin-als)序數的一種特殊子集.設a是序數,子集Aca,若對於任何序數月EA,都存在序數YEA,使月<Y,並且}JA=a,則稱A在a內...
序數乘法(multiplication of ordinals)是序數的一種運算,對任意序數α,β,γ,有:1.α·0=0;2.α·β+=(α·β)+α;3.α·γ=sup{α·β|β<γ},當...
為麻將裡面的牌型,比如說全帶五,麻將術語。每副牌及將牌必須有5的序數牌。不計斷麼。 而序數牌就是只一對以上的牌型·就是任何花色都帶有五,包括將牌。...
序數效用論 外文名 Theory Of Ordinal Utility 目的 為了彌補基數效用論的缺點 定義 效用比較通過順序或等級進行 目錄 1 學術發展 2 理論觀點 ▪ 基本觀...
定義序數時, 它有一個基本的運算是後繼運算 S來得到下一個更高的序數. 如果使用von Neumann序數(用於集合論的標準序數)表示,對於任何一個序數我們可以得到, <...
類似於集合秩的概念,利用可構造分層可定義可構造集的L秩:對任何xEL,令pCx)為使xE L甲+1)成立的最小序數月,稱之為x的L秩.L秩反映了可構造集所在的構造...
因此,就可以把良序集按序同構來分類,並將同屬於一類的稱為具有同一序型的良序集。而序數就可定義作為同構的良序集的代表。依此,可以定義序數的運算。例如,序數...
而序數就可定義作為同構的良序集的代表。依此,可以定義序數的運算。例如,序數的加法可以定義如下:若α,β為序數,γ為極限序數。即用關於α的超限歸納原理來定義...
我們可以說博雷爾代數是G,其中ω1是第一不可數序數,即勢為ℵ₁的序數集。...一個重要的例子,尤其是對於機率論而言,是實數集上的博雷爾代數。它是用來定義...
序數理論是義大利數學家G.皮亞諾提出來的。他總結了自然數的性質,用公理法給出自然數的如下定義: 自然數集N是指滿足以下條件的集合:①N中有一個元素,記作1...
重定義空集為馮·諾伊曼序數[0]。則 {[0]},僅含有元素空集的集合,屬於 S2X;定義為馮·諾伊曼序數 [1]。 類似的,{[1]} 屬於 S3X,則 {[0]} and {[...
超限遞歸是一種構造或定義某種對象的方法,它與超限歸納的概念密切相關。例如,可以定義以序數為下標的集合序列Aα,只要指定三個事項:...
對於有限數,有兩種方式考慮超限數,作為基數和作為序數。不像有限基數和序數,超限基數和超限序數定義了不同類別的數。超限數含義 編輯 1.最小超限序數是ω。...
對於包含一個可良序化的共尾子集的線性序集,定義它的共尾度為同構於它的一個共尾子集的最小序數。例如,自然數集是有理數集的可良序化的共尾子集,故有理...
[1] a有窮集(a-finite set)有窮集概念在a遞歸論中的推廣.1.。中的元素...的子集恰為自然數的姚集(關於。ck2與}2的定義,參見“可允許序數”)....
(1)對於定義的基本情況,讓 是X的開放子集的集合。(2)如果i不是一個極限序數,那么i有一個緊接在前面的序數i-1,讓(3)如果i是一個極限序數,讓...
事實上,若κ是強不可達基數,又集合X的基數|X|<κ,則冪集P(X)的基數也...1.若x是可良序化的,則定義|x|為最小的與x等勢的序數。2.若不然,則定義...
a遞歸論(a-recursion theory)一種遞歸理論.是經典遞歸論(研究。上函式與集合的能行性問題)將論域擴展到可允許序數上以後所形成的一種理論. 將經典遞歸論推廣到...
