序數可定義集是一個數學術語。
基本介紹
- 中文名:序數可定義集
- 外文名:ordinal-definable set
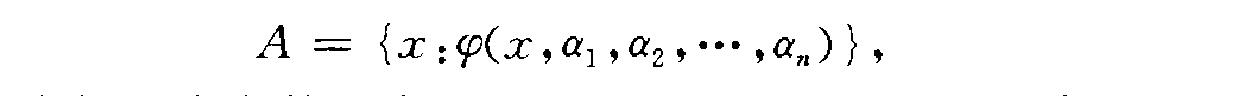
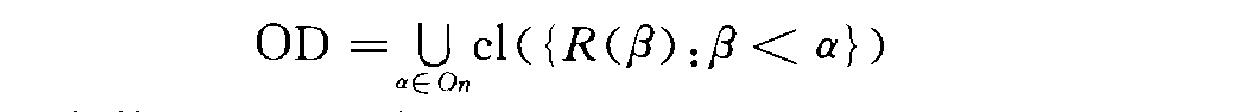
序數可定義集是一個數學術語。
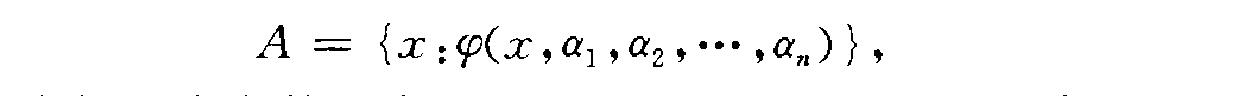
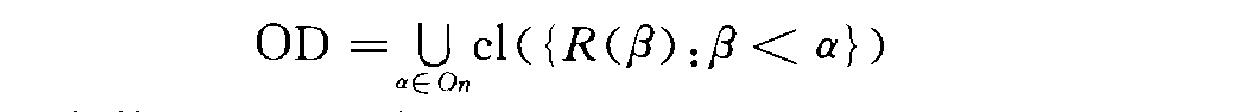
序數,為集合論基本概念之一,是日常使用的第一、第二等表示次序的數的推廣。序數概念是建立在良序集概念之上的,而良序集又是偏序集、全序集的特殊情形。定義 漢語釋義 序數,是表示次序的數目。漢語表示序數的方法較多。通常是在整數前...
序數是集合論基本概念之一。是“第一”、“第二”等表示次序的數在概念上的推廣。康托爾原來把序數定義為良序集a的序型ā,作為所有與a序同構的集的共同特徵,即與a序同構的良序集的等價類。概念 初始序數(initial ordinals number)...
定義 極限序數是一類特殊的序數。指不為0且不是後繼序數的序數。一切序數被分成三類:1.只含0這個序數。2.後繼序數。3.極限序數。ω={0,1,2,…}是最小的極限序數。序數可按順序列出如下:0,1,2,…,ω,ω+1,ω+2...
自然數集ω上的數學歸納法 (包括證明與定義) 可以自然地拓廣到任一極限序數(甚至全體序數類) 上去,稱為超窮歸納法。後者除後繼序數場合外,還須考察極限序數的場合。歸納法定義又稱遞歸定義,下以序數算術中的加法、乘法與冪的遞歸...
,這時P按上述關係是良序的,從而可以定義積 為Ord(P)。不難看出,兩種方法總是給出同一結果。對此,只須驗證:族 (這裡對於一切 ,)的分離並和附有序關係的族 (這裡 )的卡氏積是同構良序集。序數乘法的性質 序數乘法有下列性質:...
這樣可以把自然數變成了在ZF內可以定義的一種性質,如把0定義作空集═,1定義作0∪{0},2定義作1∪{1}……等等,則0,1,2,…,都是自然數,而且只有這些是自然數。自然數 “x是序數”是指如果集合x是傳遞集,而且x在∈下...
重定義空集為馮·諾伊曼序數[0]。 則 {[0]},僅含有元素空集的集合,屬於 S2X;定義為馮·諾伊曼序數 [1]。 類似的,{[1]} 屬於 S3X,則 {[0]} and {[1]} 的並集 {[0],[1]} 也屬於該集合;定義為馮·諾伊曼序數 ...
其中c1 (M)表示M的哥德爾閉包,稱Def (x)為x的可定義冪集.對任意序數a,遞歸定義集合L(a)如下,L(0)=O;L(a+1)=Def(L(a));當a為極限序數時,為可構造集全域,L中的元素稱為可構造集.可構造集全域最初由哥德爾於1938年...
這樣 ,所有單元素集{x},{y},{a},{b}等具有同一基數,記作1 。類似,凡能與兩個手指頭建立一一對應的集合,它們的基數相同,記作2,等等 。自然數的加法、乘法運算可以在序數或基數理論中給出定義,並且兩種理論下的運算是一致的。
這樣 ,所有單元素集{x},{y},{a},{b}等具有同一基數 , 記作1 。類似,凡能與兩個手指頭建立一一對應的集合,它們的基數相同,記作2,等等 。自然數的加法 、乘法運算可以在序數或基數理論中給出定義,並且兩種理論下的運算...
α階導集 α階導集(a-th derived set)導集概念的推廣.拓撲空間X的導集X“稱為X的第一階導集,記為X")=X}一般地,設a為任意序數,當a有前趨序數a-1時,記X=(X(a 1)}d;當a是極限序數時,記X}0> _自{X ...
基數和序數:在NF(和TST)中,存在n個元素的所有集合的集合(這裡循環性只是外觀上的)。所以弗雷格的基數定義在NF和NFU中可行:基數是集合在等勢關係下的等價類:集合 A 和 B 是等勢的,如果存在它們之間的雙射,在這種情況下我們寫...
