(1) 形聲。從攴( pū),婁聲。本義:點數;計算。
(2) 同本義 [count]
是一個用作計數、標記或用作量度的抽象概念，是比較同質或同屬性事物的等級的簡單符號記錄形式（或稱度量）。代表數的一系列符號，包括數字、運算符號等統稱為記數系統。在日常生活中，數通常出現在在標記（如公路、電話和門牌號碼）、序列的指標（序列號）和代碼（ISBN）上。在數學里，數的定義延伸至包含如分數、負數、無理數、超越數及複數等抽象化的概念。
起初人們只覺得某部分的數是數，後來隨著需要，逐步將數的概念擴大；例如畢達哥拉斯認為，數必須能用整數和整數的比表達的，後來發現無理數無法這樣表達，引起第一次數學危機，但人們漸漸接受無理數的存在，令數的概念得到擴展。
基本介紹
誕生及發展,自然數,分類,序數理論,基數理論,數的分類,數的存儲格式,
誕生及發展
“數”是量度事物的概念。是客觀存在的量的意識表述。”數字“起源於原始人類用來數數計數的記號形成自然數“數”的符號，是人類最偉大的發明之一，是人類精確描述事物的基礎。在人類漫長的歷史進程中，
1° 通過對現實事物數數這種方式得到了數；
2° 數可以使用一定的方式進行運算；
3° 數同空間事物相聯繫時，可表明這些事物的多少。（摘自自然數原本數數論）
若干年以前，人類的祖先為了生存，往往幾十人在一起，過著群居的生活。他們白天共同勞動，搜捕野獸、飛禽或採集果薯食物；晚上住在洞穴里，共同享用勞動所得。在長期的共同勞動和生活中，他們之間逐漸到了有些什麼非說不可的地步，於是產生了語言。他們能用簡單的語言夾雜手勢，來表達感情和交流思想。隨著勞動內容的發展，他們的語言也不斷發展，終於超過了一切其他動物的語言。其中的主要標誌之一，就是語言包含了算術的色彩。
後來，群居發展為部落。部落由一些成員很少的家庭組成。所謂“有”，就分為“一”、“二”、“三”、“多”等四種（有的部落甚至連“三”也沒有）。任何大於“三”的數量，他們都理解為“多”或者“一堆”、“一群”。有些酋長雖是長者，卻說不出他捕獲過多少種野獸，看見過多少種樹，如果問巫醫，巫醫就會編造一些辭彙來回答“多少種”的問題，並煞有其事地吟誦出來。然而，不管怎樣，他們已經可以用雙手說清這樣的話（用一個指頭指鹿，三個指頭指箭）：“要換我一頭鹿．你得給我三枝箭。”這是他們當時沒有的算術知識。
大約在1萬年以前，冰河退卻了。一些從事遊牧的石器時代的狩獵者在中東的山區內，開始了一種新的生活方式──農耕生活。他們碰到了怎樣的記錄日期、季節，怎樣計算收藏穀物數、種子數等問題。特別是在尼羅河谷、底格里斯河與幼發拉底河流域發展起更複雜的農業社會時，他們還碰到交納租稅的問題。這就要求數有名稱。而且計數必須更準確些，只有“一”、“二”、“三”、“多”，已遠遠不夠用了。
底格里斯河與幼發拉底河之間及兩河周圍，叫做美索不達米亞，那兒產生過一種文化，與埃及文化一樣，也是世界上最古老的文化之一。美索不達米亞人和埃及人雖然相距很遠，但卻以同樣的方式建立了最早的書寫自然數的系統──在樹木或者石頭上刻痕劃印來記錄流逝的日子。儘管數的形狀不同，但又有共同之處，他們都是用單劃表示“一”。
後來（特別是以村寨定居後），他們逐漸以符號代替刻痕，即用1個符號表示1件東西，2個符號表示2件東西，依此類推，這種記數方法延續了很久。大約在5000年以前，埃及的祭司已在一種用蘆葦製成的草紙上書寫數的符號，而美索不達米亞的祭司則是寫在鬆軟的泥板上。他們除了仍用單劃表示“－”以外，還用其它符號表示“+”或者更大的自然數；他們重複地使用這些單劃和符號，以表示所需要的數字。
公元前1500年，南美洲秘魯印加族（印第安人的一部分）習慣於“結繩記數”──每收進一捆莊稼，就在繩子上打個結，用結的多少來記錄收成。“結”與痕有一樣的作用，也是用來表示自然數的。根據我國古書《易經》的記載，上古時期的中國人也是“結繩而治”，就是用在繩上打結的辦法來記事表數。後來又改為“書契”，即用刀在竹片或木頭上刻痕記數．用一划代表“一”。直到今天，我們中國人還常用“正”字來記數．每一划代表“一”。當然，這個“正”字還包含著“逢五進一”的意思。
自然數
在數東西的時候，數出的0、1、2、3、4、5、6、7、8、9、…叫自然數。
自然數有數量、次序兩層含義，分為基數、序數。基本單位為1，計數單位有個、十、百、千、萬等
分類
按“能否被2整除”可分為：奇數、偶數。
按“因數個數”可分為：質數、合數。
用以計量事物的件數或表示事物次序的數。即用數碼0，1，2，3，4，…所表示的數。自然數由0開始，一個接一個，組成一個無窮集體。自然數集有加法和乘法運算，兩個自然數相加或相乘的結果仍為自然數，也可以作減法或除法，但相減和相除的結果未必都是自然數，所以減法和除法運算在自然數集中並不是總能成立的。自然數是人們認識的所有數中最基本的一類，為了使數的系統有嚴密的邏輯基礎，19世紀的數學家建立了自然數的兩種等價的理論棗自然數的序數理論和基數理論，使自然數的概念、運算和有關性質得到嚴格的論述。
序數理論
是義大利數學家皮亞諾（Giuseppe Peano）提出來的。他總結了自然數的性質，用公理法給出自然數的如下定義。
自然數集N是指滿足以下條件的集合：
Ⅰ N中有一個元素，記作1。
Ⅱ N中每一個元素a都能在 N 中找到一個元素作為它的後繼者，記作a'。
Ⅲ 0'=1。
Ⅳ 0不是任何元素的後繼者。
Ⅴ 不同元素有不同的後繼者。
Ⅵ （歸納公理）對於N的任一子集M，如果1∈M，並且只要a在M中就能推出a'也在M中，那么M=N。
基數理論
自然數在日常生活中起了很大的作用，人們廣泛使用自然數。自然數是人類歷史上最早出現的數，自然數在計數和測量中有著廣泛的套用。人們還常常用自然數來給事物標號或排序，如城市的公共汽車路線，門牌號碼，郵政編碼等。
“0”是否包括在自然數之記憶體在爭議，有人認為自然數為正整數，即從1開始算起；而也有人認為自然數為非負整數，即從0開始算起。關於這個問題尚無一致意見。不過，在數論中，多採用前者；在集合論中，則多採用後者。我國中國小教材將0歸為自然數。
自然數是整數，但整數不全是自然數。
例如：-1，-2，-3，...是整數，而不是自然數。
總之一句話自然數就是大於等於0的整數。
全體非負整數組成的集合稱為非負整數集（即自然數集）。
數的分類
我們把0、1、2、3、4、5、6、7、8、9、10、…等全體非負整數組成的數稱為“自然數”。把1，2，3，…，9，10向前擴充得到正整數1，2，3，…，9，10，11，…，把它反向擴充得到負整數…，-11，-10，-9，…，-3，-2，-1 ，介於正整數和負整數中間的“0”為中性數；把它們合在一起，得到…，-11，-10，-9，…，-3，-2，-1，0，1，2，3，…，9，10，11，…， 叫做整數。對整數可以施行加、減、乘、除四種運算，叫做四則運算。整數，對加、減、乘運算組成了一個封閉的數集合，是數學古老分支“數論”研究的對象。著名的德國數學家高斯說：“數學是科學的皇后，數論是數學中的皇冠”。除法運算，如7/11 = 0.636363 …、11/7 = 1.5714285 …，不再是整數，也就是說整數對除法運算是不封閉的。為了使數集合對加、減、乘、除四則運算都是封閉的，就必須增加新的數，如7/11、11/7，為兩個整數之比，稱為可比數、分數，現 在通稱為有理數。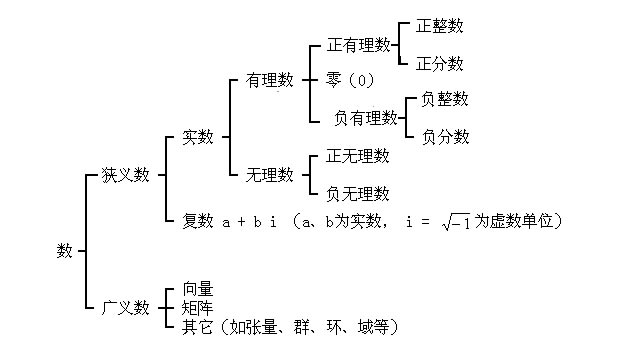
把數的性質、數和數之間的四則運算在套用過程中的經驗進行總結和整理，形成最古老的一門數學——算術。有理數集合，對加、減、乘、除四則運算組成了一個封閉的數集合，看起來似乎已很完備。2500多年前，不少人、甚至當時一些數學家也是這樣看的。
公元前5世紀，當時的畢達哥拉斯學派很重視整數，想用它說明一切，“數是萬物之本”成了他們的哲學觀。無理數的發現，對以整數為基礎的畢氏哲學，是一次致命的打擊，數學史上把這件事稱為“第一次數學危機”。在之後，又發現了很多無理數，圓周率π就是其中最重要的一個。15世紀義大利著名畫家達·文西把它稱之為“無理之數”。現 在，人們把有理數和無理數合併在一起，稱為“實數”。由此得到兩個解：和，它們還是（2）的解嗎？如果認為不是，（2）就沒有解，解方程如同走進了死胡同。為解決這一問題，數學家不得不再次擴大數的範圍，引入符號“i”表示“－1的平方根”，即 
，稱為虛數；再把實數a、b和虛數結合起來，組成形式的數，稱為“複數”。在很長一段時間裡，人們在實際生活中找不到用虛數和複數表示的量，讓人感到有點虛無縹緲。隨著科學的發展，虛數在水力、繪圖、航空等領域中得到了廣泛的套用。這樣，數的家族就進一步擴大，包括實數和虛數兩大類，並把加、減、乘、除的擴展到包括乘方和開方的，形成了數學中一個新的分支“代數”。代數進一步向兩個方面發展，一是研究未知數更多的一次方程組，引進矩陣、向量、空間等符號和概念，形成“線性代數”；另一是研究未知數次數更高的高次方程，形成“多項式代數”（也叫“多項式理論”）。這樣，代數研究的對象，不僅是數，還包括矩陣、向量、向量空間及其變換等。它們都可以進行“運算”，雖然也叫做加法或乘法，但是關於數的基本運算定律，有時不再有效。因此，代數學的內容可以概括稱為帶有運算的一些代數結構的集合，如群、環、域等，又含抽象代數、布爾代數、關係代數、計算機代數等眾多分支.由於科學技術發展的需要，數的範圍不斷擴大，從正整數、自然數、整數、實數到複數，再到向量、張量、矩陣、群、環、域等不斷的擴充與發展。為區別起見，人們把實數和複數稱為“狹義數”，把向量、張量、矩陣等稱為“廣義數”。儘管人們對數如何分類還有一些不同的看法，但都承認數的概念還會不斷擴充和發展。
數的存儲格式
數的存儲格式也就是數字的存儲順序。在表示數值的大小時，一個位元組(byte)最大只能表示255(0xFF),這也是遠遠不夠 的。為了滿足實際的使用需要，通常會使用2個，4個或者8個位元組(byte)來表示數值的大小。對於使用多位元組表示數值的情況 ,就 存在一個順序問題。數的存儲順序有兩種——Big-endian(大頭位序)格式和Little-endian(小頭序列)。
漢字文化圈記數新法
| 千退位·微觀小數 | 千進位·巨觀大數 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
源自宋朝謝察微·《算經》 | 源自南北朝·《孫子算經》 | 源自漢朝徐岳·《數術記遺》 | |||||||||
渺 10-33 | 十渺 10-32 | 百渺 10-31 | 忽 10-15 | 十忽 10-14 | 百忽 10-13 | 千 103 | 十千 104 | 百千 105 | 秭 1021 | 十秭 1022 | 百秭 1023 |
埃 10-30 | 十埃 10-29 | 百埃 10-28 | 絲 10-12 | 十絲 10-11 | 百絲 10-10 | 萬 106 | 十萬 107 | 百萬 108 | 穰 1024 | 十穰 1025 | 百穰 1026 |
塵 10-27 | 十塵 10-26 | 百塵 10-25 | 毫 10-9 | 十毫 10-8 | 百毫 10-7 | 億 109 | 十億 1010 | 百億 1011 | 溝 1027 | 十溝 1028 | 百溝 1029 |
沙 10-24 | 十沙 10-23 | 百沙 10-22 | 厘 10-6 | 十厘 10-5 | 百厘 10-4 | 兆 1012 | 十兆 1013 | 百兆 1014 | 澗 1030 | 十澗 1031 | 百澗 1032 |
纖 10-21 | 十纖 10-20 | 百纖 10-19 | 分 10-3 | 十分 10-2 | 百分 10-1 | 京 1015 | 十京 1016 | 百京 1017 | 正 1033 | 十正 1034 | 百正 1035 |
微 10-18 | 十微 10-17 | 百微 10-16 | 個 100 | 十個 101 | 百個 102 | 垓 1018 | 十垓 1019 | 百垓 1020 | 載 1036 | 十載 1037 | 百載 1038 |
