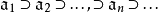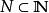相關詞條
- 阿廷環
阿廷環是抽象代數中一類滿足降鏈條件的環,以其開創者埃米爾·阿廷命名。...... 阿廷環是抽象代數中一類滿足降鏈條件的環,以其開創者埃米爾·阿廷命名。 [1] ...
- 左(右)阿廷環
左(右)阿廷環(lift (right) Artinian ring)一類具有降鏈條件的環.它是阿廷(Artin,E.)引人的.對左(右)理想滿足降鏈條件(或說對左(右)理想滿足極小條件)...
- 克魯爾環
克魯爾環(Krull ring)以克魯爾命名的一類重要的整環,戴德金整環、一般的整閉諾特整環都是克魯爾環。...
- 科恩-麥考利環
在交換代數中,科恩-麥考利環是對應到一類代數幾何性質(例如局部等維性)的交換環。...... 有理奇點對應到 Cohen-Macaulay 環,卻不一定是 Gorenstein 環。 阿廷環...
- 克魯爾維數
克魯爾維數(Krull dimension)是決定環結構的一個參數,對賦值環的研究有重要意義。設p是R的素理想,R中終止於p的素理想真升鏈p0⊂p1⊂…⊂pn=p的長度n的...
- 完全環
完全環(perfect ring)是一類具有同調性質的環,概念是巴斯(Bass , H.)於1960年研究模範疇的同調性質時引進的。環是對並與差運算封閉的集類,測度論中重要概念之...
- 森田等價
在抽象代數中,森田等價(Morita equivalence)是定義在環之間的一個等價關係,這個等價保持許多環論性質。以日本數學家森田紀一(Kiiti Morita)命名,他在1958年定義了...
- 半完全環
半完全環是介於完全環與半局部環之間的一類環。設J(R)是環R的雅各布森根,若R/J (R)是半單環,且R/J (R)的冪等元可提升為R的冪等元,則稱R為半完全...
- 諾特模
諾特模是抽象代數中一類滿足升鏈條件的模,定義方式類似諾特環。是一種重要的模。它是阿廷模的對偶概念。即滿足極大條件的模。若A模M的任一子模升鏈M1M2…都...
- 群代數半單性定理
環R是半單阿廷環若且唯若左(右)正則模是半單模。常簡稱半單環.著名的韋德伯恩-阿廷定理給出:R是半單環的充分必要條件是R為有限個單阿廷環的直和,若不計...
- 不動環
不動環,((fixed ring)由不動域引申的概念...... 1單環,G作用是外自同構,則‘浪是本原環;若R是半單阿廷環,且一G}一‘ER,則“R也是半單阿廷環.不動環...
- 余諾特環
余諾特環(co-Noetherian ring)諾特環的對偶.稱環R是左余諾特(阿廷)的,若環R滿足以下等價條件之一: 1. R-mod有阿廷(諾特)餘生成子. 2.任意有限餘生成左R...
- 素環
素環是一類重要的環。若環R的零理想是素理想,則稱R為素環。整環、單環、本原環都是素環。素環與素理想有如下關係:P是R的素理想若且唯若R/P是素環。....
- 扎里斯基中心環
扎里斯基中心環(Zariski central ring)一種拓撲裝置的特殊環。...... 半單阿廷環、阿茲瑪亞代數、分次除環均為扎里斯基中心環.設R是 G分次環,若R也為扎里斯基中...
- 半素環
半素環是一類重要的環。若環 R 的零理想是半素理想,則稱R為半素環。環R是半素的充分必要條件是:R的貝爾根為零,或R無非零的冪零理想。半素環恆為素環的...