基本介紹
- 中文名:阿基米德螺線
- 外文名:Archimedean spiral
- 別名:阿基米德曲線
- 提出者:阿基米德
- 提出時間:公元前三世紀
- 套用學科:數學
數學表達

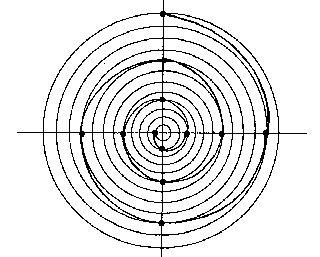









幾何畫法
歷史沿革


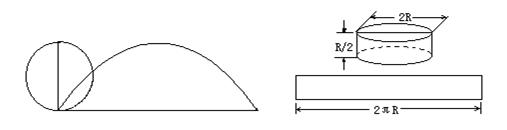
自然界中螺線
套用



阿基米德螺旋線一般指本詞條
















數學中有各式各樣富含詩意的曲線,螺旋線就是其中比較特別的一類。螺旋線這個名詞來源於希臘文,它的原意是“旋卷”或“纏卷”。例如,平面螺旋便是以一個固定點開始向外逐圈旋繞而形成的曲線。在2000多年以前,古希臘數學家阿基米德...
對於平面螺線,是指在平面極坐標系中,如果極徑ρ隨極角θ的增加而成比例增加(或減少),這樣的動點所形成的軌跡。典型的螺線有球面螺旋線、阿基米德螺線、對數螺線、雙曲螺線等。球面螺旋線 球面螺旋線是一種常見的曲線,屬於螺旋線的...
阿基米德螺旋、漸開線螺旋、風螺旋、C螺旋、自由螺旋 均屬於等距螺旋。等距螺旋的分類 直線運動與圓周運動的位置關係可以分為五類:直線與圓相切於頂部。直線與圓相交於上半部。直線穿過圓心。直線與圓相交於下半部。直線與圓相切於底部。
阿基米德蝸桿(ZA蝸桿): 這種蝸桿,在垂直於蝸桿軸線的平面(即端面)上,齒廓為阿基米德螺旋線,在包含軸線的平面上的齒廓(即軸向齒廓)為直線,其齒形角α₀=20°。它可在車床上用直線刀刃的單刀(當導程角γ≤3°時)或雙刀...
阿基米德圓柱蝸桿又稱ZA型蝸桿;齒面為阿基米德螺旋面的圓柱蝸桿。一、阿基米德圓柱蝸桿的定義 其端面齒廓為阿基米德螺旋線;軸向齒廓為直線。二、阿基米德圓柱蝸桿的加工原理 車制,車刀切削刃通過蝸桿軸線的直線。這種蝸桿在在軸向剖面A-A上...
它的螺旋角為常數。很容易證明,這種彈簧的教面重心所引起的表面為拋物線迴轉.這種螺旋線在坐標角為0至φ的區城中(即由r至r)的弧長S,等於:阿基米德螺旋線的總長S的求法與前同。故彈簧線的長度為:
螺旋線屬線粒體恰型線,生物斜型螺的維度區,在腹腔型軟體動物,有DNA數據線中存線上粒體恰型線一條或更多。螺旋線,或者稱為螺線。按維度分可以分為二維螺旋線,和三維螺旋線。二維螺旋線包括:阿基米德螺線 費馬螺線 等角螺線 雙...
旋卷”或“纏卷”。例如,平面螺旋便是以一個固定點開始向外逐圈旋繞而形成的曲線。在2000多年以前,古希臘數學家阿基米德就對螺旋線進行了研究。著名數學家笛卡爾於1683年首先描述了對數螺旋線,並且列出了螺旋線的解析式。
數學曲線阿基米德螺旋曲線 直角坐標系方程:暫無 極坐標系方程:ρ=a*θ面積公式:暫無周長公式:暫無數學曲線四葉草曲線 直角坐標系方程:暫無 ;極坐標線方程:ρ=sin(θ)*cos(θ)面積公式:4周長公式:暫無...
為阿基米德螺旋線。這種蝸桿加工測量方便。缺點是齒面不易磨削,不能採用硬齒面,傳動效率低。通常將通過蝸桿軸線並垂直於蝸輪軸線的平面稱為中間平面。在此平面上,蝸桿與蝸輪的嚙合類似於齒條與齒輪的嚙合,如圖5所示,蝸桿傳動的主要...
圓柱蝸桿傳動是蝸桿分度曲面為圓柱面的蝸桿傳動。其中常用的有阿基米德圓柱蝸桿傳動和圓弧齒圓柱蝸桿傳動。①阿基米德蝸桿的端面齒廓為阿基米德螺旋線,其軸面齒廓為直線。阿基米德蝸桿可以在車床上用梯形車刀加工,所以製造簡單,但難以磨削,故...
平均曲率半徑法求阿基米德螺旋線的代用圓弧 機械工程中,阿基米德螺旋線是一種最常用的曲線。代用圓弧的求法通常有兩種:①三點共圓法:即在要替代的一段曲線上,取三點(通常是起點、中點、及終點)作一圓;②最小二乘法圖:使整段...
當從動桿按等速運動規律運動,凸輪按等角速度迴轉,此時畫出的凸輪輪廓曲線是阿基米德螺旋線。其作圖方法:①以O₁為圓心,O₁O₂為半徑畫一圓,截取圓心角中¨ 並等分為四等分,②延長O₁O₂至4點令O₂4等於導程h,並...
為了避免微動手輪上的精密螺紋(或其他微動機構)磨損,有的顯微鏡把可動分劃板上的雙刻線製成雙阿基米德螺旋線(概述圖中c)。雙阿基米德螺旋線的螺距等於1/10線紋尺線紋間距乘以物鏡放大倍數,而在其內圈又刻有100個等分分度,所以在它...
耐高溫抗老化矽膠編織線 低噪音電機,帶過熱保護 阿基米德螺旋線風道,大排氣量,超靜音 產品類型:光暖浴霸 安裝方式:吸頂式 額定功率:1130W 電源規格:220V/50Hz 安裝開孔尺寸:300*300mm 其他性能:耐高溫PC面板+1mm鋁板噴砂陽極...
滾刀阿基米德蝸桿 滾刀 阿基米德蝸桿的螺旋齒側面是阿基米德螺旋面。通過蝸桿軸線剖面與阿基米德蝸螺旋面的交線是直線,其它剖面都是曲線,其端剖面是阿基米德螺旋線。用這種基本蝸桿製成的滾刀,製造與檢驗滾刀齒形均比漸開線蝸桿簡單和方便。但...
其他性能:1、耐溫PC面板, 美觀高檔2、金色防水防爆紅外取暖燈泡, 安全3、低噪音電機, 帶過熱保護4、照明、取暖互鎖防水開關, 安全節能5、智慧型過熱保護電路, 安全6、仿飛泡(40W), 美觀7、165MM超薄鐵箱體8、阿基米德螺旋線風道, 超...
當圓鋸、帶鋸及平刨、壓刨切削工件時,進給運動和純切削運動同時發生,其切削運動為二者的合成運動,切削過程的運動軌跡為合成運動的軌跡,如平、壓刨切削時的軌跡為擺線;車削時的軌跡為螺旋線,旋切時的軌跡為阿基米德螺旋線。當框鋸或...
阿基米德(公元前287年至公元前212年)通過考慮沿著曲線移動的點的路徑,發現了阿基米德螺旋線的切線。在16世紀30年代,費馬公司開發了足夠的技術來計算分析中的切線和其他問題,並用它來計算拋物線的切線。他的技巧和 和 之間的差除以h是...
轉盤共[聚]焦顯微鏡(spinning-disk confocal microscope,Nipkow disk confocal microscope)是2018年公布的生物物理學名詞。 定義 利用來自弧光燈的光通過一對高速旋轉的圓盤照射樣品,靠近光源的盤面上沿阿基米德螺旋線排列了幾千甚至上萬...
阿基米德蝸桿 阿基米德蝸桿(ZA蝸桿) 這種蝸桿,在垂直於蝸桿軸線的平面(即端面)上,齒廓為阿基米德螺旋線(圖1),在包含軸線的平面上的齒廓(即軸向齒廓)為直線,其齒形角α0=20°。它可在車床上用直線刀刃的單刀(當導程角γ...
宇宙線太陽調製,主要表現在宇宙線的日球傳播、空間梯度、日球各向異性、太陽周調製和短期調製等方面。正文 宇宙線的日球傳播 宇宙線在日球的傳播包括以下幾種過程:擴散 宇宙線粒子在行星際空間繞大尺度阿基米德螺旋線狀磁場運動時,...
從刀盤整體受力出發,並基於阿基米德螺旋線方法進行切刀布置。最後通過ANSYS Workbench有限元軟體對布置結果進行仿真分析,驗證了該方法布置刀具的合理性和有效性,表明最佳化後的方案更符合工程實際需要。
2.阿基米德蝸桿 阿基米德蝸桿的螺旋齒側面是阿基米德螺旋面。通過蝸桿軸線剖面與阿基米德蝸螺旋面的交線是直線,其它剖面都是曲線,其端剖面是阿基米德螺旋線。用這種基本蝸桿製成的滾刀,製造與檢驗滾刀齒形均比漸開線蝸桿簡單和方便。但有...
4 圓截面螺旋形密封彈簧 –具有低等彈性/變形特性的彈簧組件 5 機械密封彈簧 (波形彈簧﹐超波形彈簧和壓縮彈簧)螺旋推進器和計量螺旋 螺旋推進器是一種利用阿基米德螺旋線物理原理的柔性運輸組件﹐它是用彈簧鋼製成。在一個可彎曲...
優勢:阿基米德螺旋線蝸殼朧煙,不沾油納米台面 功能:油煙機+煤氣灶+左消毒櫃+右蒸烤箱 適合人群:智慧型高端廚房、專業玩家級烹飪 CIARRA集成灶將吸油煙機、燃氣灶、烤箱、蒸箱、恆溫置物台等功能融合為一體,專業級料理蒸烤箱。AKZ03#...
其後面用鏟削(或鏟磨)方法加工成阿基米德螺旋線的齒背,銑刀用鈍後只須重磨前面,能保持原有齒形不變,用於製造齒輪銑刀等各種成形銑刀。使用方法 銑刀的裝夾 加工中心用銑刀大多接納彈簧夾套裝夾方式,使用時處於懸臂形態。正在銑削加工...
