連續統基數(cardinal number of the continuum)亦稱連續統的勢,一個特殊的不可數基數,即實直線的基數稱為連續統基數,記為叢或。
基本介紹
- 中文名:連續統基數
- 外文名:Number of consecutive bases
- 學科:數學
- 性質:連續統的勢
背景

概念
性質
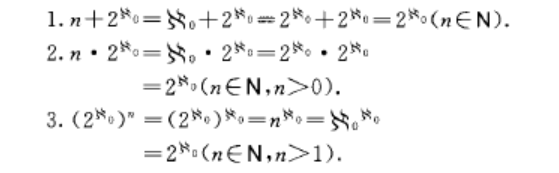

連續統基數(cardinal number of the continuum)亦稱連續統的勢,一個特殊的不可數基數,即實直線的基數稱為連續統基數,記為叢或。

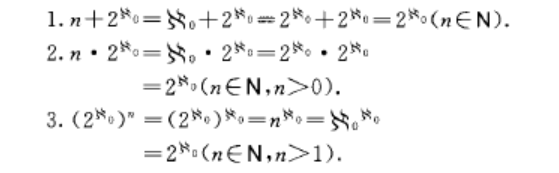
連續統基數(cardinal number of the continuum)亦稱連續統的勢,一個特殊的不可數基數,即實直線的基數稱為連續統基數,記為叢或。背景集合論的創建者Cantor驚人的創造了超限基數與超限序數。對...
連續統的基數 康托的連續統假設有時會被敘述成“在連續統的基數和自然數的基數之間不存在任何基數”,這裡的“連續統”指的是實數集;連續統的基數即特指實數集的基數。拓撲學 在點集拓撲學中,一個連續統是指任何非空的緊緻連通度量空間(或者非空的緊緻連通豪斯多夫空間,但較少用)。按照以上定義,一個單...
《連續統基數不變數研究》是依託四川大學,由張樹果擔任項目負責人的面上項目。項目摘要 在徹底解決了關於逆對偶基數不變數的幾個公開問題的基礎上,繼續深入探討幾個新的基數不變數的性質及它們與經典連續統基數不變數之間的關係問題。我們將著重研究逆對偶獨立數ic與獨立數i的關係問題,及i的共尾數可數是否與經典...
《連續統的基數特性研究》是依託四川大學,由張樹果擔任項目負責人的面上項目。項目摘要 本項目通過公理集合論中幾個重要問題的研究,特別是對極分拆關係問題、無窮基數上的理想特性和實數直線的基數特性問題的研究,揭示了兩種重要析分拆關係之間的密切聯繫,及逆對偶基數不變數之間的重要關係,並給出了連續統的關於...
.(2)一般地,當k是連續統的一個基數不變數時,考察基數不超過k的Lindelof空間是否都是D-空間...由於連續統的許多基數不變數之間的關係尚不明了,所以以上問題的解決無論是對D-空間理論還是對連續統基數的進一步研究都具有重要理論意義。結題摘要 上世紀七十年代,著名數學家Eric van Douwen提出了“正則...
初等基數 初等基數(elementary特殊基數的統稱。初等基數特殊基數的統稱.可數集Acardinal number)三種冪集}(A)的基數2氣一叢的基數}o,可數集A的,以及}(}'o(A))的基數2}統稱初等基數.這三個基數中叭。是自然數集的基數,2九為連續統基數,而2}是實數集上的一切實函式的集合的基數,它們的關係是乒0 ...
另外,連續統一詞有時即指實數線或者實數集,這是較舊的叫法;見連續統假設。康托的連續統假設有時會被敘述成“在連續統的基數和自然數的基數之間不存在任何基數”,這裡的“連續統”指的是實數集;連續統的基數即特指實數集的基數。相關研究 極限與連續是微積分最為基礎的概念,也是高等數學必教必學的內容之一...
按研究計畫我們對連續統的奇異子集進行了深入研究得到如下結果: 1.我們引入了研究自然數上理想的新的基數不變數non**(I), 我們證明此基數不變數正好刻畫了I-超濾的兼納存在性。同時我們還確定了一些具體的理想的這個基數不變數,如non**(fin×fin)=d and non**(ED)=cov(M)等. 此項研究結果發表在《中國...
(1)康托的連續統基數問題。1874年,康托猜測在可數集基數和實數集基數之間沒有別的基數,即著名的連續統假設。1938年,僑居美國的奧地利數理邏輯學家哥德爾證明連續統假設與ZF集合論公理系統的無矛盾性。1963年,美國數學家科恩(P.Choen)證明連續統假設與ZF公理彼此獨立。因而,連續統假設不能用ZF公理加以證明。在...
(1)康托的連續統基數問題。1874年,康托猜測在可數集基數和實數集基數之間沒有別的基數,即著名的連續統假設。1938年,僑居美國的奧地利數理邏輯學家哥德爾證明連續統假設與ZF集合論公理系統的無矛盾性。1963年,美國數學家科思(P.Choen)證明連續統假設與ZF公理彼此獨立。因而,連續統假設不能用ZF公理加以證明。在...
f空間的 extent是否具有連續統基數問題及是否存在(a)-Dowker空間問題,同時研究在一定拓撲性質下的不同星覆蓋性質的表現形式等問題。研究單調覆蓋性質、單調正規的仿緊空間及序數有限積空間的子空間的對偶性質。研究樹及其子空間的性質並研究一樹是D-空間的等價條件。研究某些特殊空間類的D-空間性質及具有D-性質的某些...
752 021 072 936 960 章 數獨 359 第2^(57 885 161)-1 章 已知最大的質數 362 第八篇 無窮數 367 第 0 章 阿列夫零:最小的無窮大 369 第C 章 連續統基數 378 第九篇 生命、宇宙和…… 383 第42 章 42,一點都不乏味 385 人名對照表 392 推薦閱讀 404 圖片著作權 406 著作權聲明 407 ...
(1)康托的連續統基數問題。(2)算術公理系統的無矛盾性。(3)只根據契約公理證明等底等高的兩個四面體有相等之體積是不可能的。(4)兩點間以直線為距離最短線問題。(5)拓撲學成為李群的條件(拓撲群)。(6)對數學起重要作用的物理學的公理化。(7)某些數的超越性的證明。(8)素數分布問題,尤其對...
12 基數 6 121 可數基數 7 122 連續統基數 9 123 基數的比較 10 13 集論發展簡史 14 第2 章度量空間 17 21 一致連續性與一致收斂性 17 211 一致連續性 17 212 一致收斂性 25 22 度量空間的概念和例子 27 221 度量空間的概念 27 222 HÄolder 不等式和Mnkowsk 不等式 28 223 度量空間的例子 30 ...
