①一個整數能夠被另一個整數整除,這個整數就是另一整數的倍數。如15能夠被3或5整除,因此15是3的倍數,也是5的倍數。
②一個數除以另一數所得的商。如a÷b=c,就是說,a是b的倍數。例如:A÷B=C,就可以說A是B的C倍。
③一個數的倍數有無數個,也就是說一個數的倍數的集合為無限集。 注意:不能把一個數單獨叫做倍數,只能說誰是誰的倍數。
基本介紹
- 中文名:倍數
- 外文名:multiple
- 定義:一個整數能夠被另一整數整除
- 規律:任意兩個奇數的平方差是8的倍數
①一個整數能夠被另一個整數整除,這個整數就是另一整數的倍數。如15能夠被3或5整除,因此15是3的倍數,也是5的倍數。
②一個數除以另一數所得的商。如a÷b=c,就是說,a是b的倍數。例如:A÷B=C,就可以說A是B的C倍。
③一個數的倍數有無數個,也就是說一個數的倍數的集合為無限集。 注意:不能把一個數單獨叫做倍數,只能說誰是誰的倍數。
①一個整數能夠被另一個整數整除,這個整數就是另一整數的倍數。如15能夠被3或5整除,因此15是3的倍數,也是5的倍數。 ②一個數除以另一數所得的商。如a÷b=...
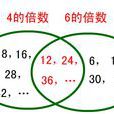
公倍數(common multiple)是指在兩個或兩個以上的自然數中,如果它們有相同的倍數,這些倍數就是它們的公倍數。公倍數中最小的,就稱為這些整數的最小公倍數(...
指的是在分析兩個分數的大小時,通過分析兩個分子的倍數與兩個分母的倍數的大小,從而得到兩個分數大小的方法。...
膨脹倍數是指物料膨脹後與膨脹前鬆散體積之比值。...... 膨脹倍數是指物料膨脹後與膨脹前鬆散體積之比值。中文名 膨脹倍數 外文名 expansion ratio 概念 物料膨...
兩個或多個整數公有的倍數叫做它們的公倍數,其中除0以外最小的一個公倍數就叫做這幾個整數的最小公倍數。整數a,b的最小公倍數記為[a,b],同樣的,a,b...
企業倍數 Enterprise Multiple 定義: 評估公司價值的指標。企業倍數估值從潛在收購方的角度評估公司的價值,估價過程中包含了債務,而其他估值倍數,例如市盈率則沒有包含...
截流倍數是指合流制排水系統在降雨時截留的雨水量與旱流污水量之比值。不從截流井瀉出的雨水量,這個指定倍數稱為截流倍數。...
電壓放大倍數是指放大電路輸出電壓與輸入電壓之比...... 電壓放大倍數公式 編輯 設為正弦輸入輸出,Ui為輸入電壓,Uo為輸出電壓,則電壓放大係數Au=Uo/Ui 。V百科往...
認購倍數 含義 用有效申購總股數除以獲配總股數 作用 申購總股數 詞性 名詞就是用有效申購總股數除以獲配總股數。詞條標籤: 科學 V百科往期回顧 詞條統...
在SI基本單位前加詞頭用於構成倍數單位(十進倍數單位和分數單位),但不得單獨使用。...... 在SI基本單位前加詞頭用於構成倍數單位(十進倍數單位和分數單位),但不得...
股票倍數,英文名稱Equity Multiplier,是股票常用術語,計算方法是股票倍數=總資產÷普通股總股本...
融資性放大倍數反映出融資性擔保公司業務狀況。...... 融資性放大倍數反映出融資性擔保公司業務狀況。擔保融資性放大倍數=融資性擔保責任餘額[1] /淨資產。融資性擔...
濃縮倍數(concentration times):在循環冷卻水中,由於蒸發而濃縮的物質含量與補充水中同一物質含量的比值,或指補充水量與排污水量的比值。...
利息保障倍數(interest coverage ratio),又稱已獲利息倍數(或者叫做企業利息支付能力比較容易理解),是指企業生產經營所獲得的息稅前利潤與利息費用的比率(企業息稅前...
倍數4編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!亦稱“四倍躍進”。出自同名專著《四倍躍進》(1997)一書。一種...
超額認購倍數就是指證券市場發行股票或債券時投資者實際參與購買該公司的股票或債券金額與預先確定發行金額的比率。...
《5的倍數 Five-O Free》是一款算術益智類遊戲。...... 《5的倍數 Five-O Free》是一款算術益智類遊戲。目錄 1 遊戲簡介 2 更新提示 5的倍數遊戲簡介 編輯 ...
稀釋被倍數法是測定時,去除樹葉、枯枝等雜物後,先用文字描述水樣顏色的種類和深淺程度。然後取一定量水樣,用蒸餾水稀釋到剛好看不到顏色,根據稀釋倍數表示該水樣的...
三極體的電流放大倍數又稱三極體的電流分配係數,字母為希臘字母β;在三極體的三個電流中,有一個電流發生變化,另外兩個電流也會隨著按比例地變化。例如,基極電流Ib的...
數碼攝像機的光學變焦方式與傳統35mm相機差不多,就是通過鏡片移動來放大與縮小需要拍攝的景物,光學變焦倍數越大,能拍攝的景物就越遠。...
電壓放大倍數、輸入電阻和輸出電阻是放大電路的三個主要性能指標,分析這三個指標最常用的方法是微變等效電路法,這是一種在小信號放大條件下,將非線性的三極體放大...
權益乘數又稱股本乘數,是指資產總額相當於股東權益的倍數。 權益乘數越大表明所有者投入企業的資本占全部資產的比重越小,企業負債的程度越高;反之,該比率越小,...
含義:差倍問題即已知兩數之差和兩數之間的倍數關係,求出兩數。公式:差÷(倍數-1)=小數;小數×倍數=大數。...
已知兩個數的和與兩個數的倍數關係,求兩個數各是多少的套用題,我們通常叫做和倍問題。解答此類套用題時要根據題目中所給的條件和問題,畫出線段圖,使數量關係一...
國際單位制按一貫計量單位制的原則構成,採用十進制構成其倍數和分數單位;只能通過SI詞頭構成倍數和分數的單位,其基本單位及其定義只能由國際計量大會決定,SI導出單位的...
