初等基數(elementary特殊基數的統稱。
基本介紹
- 中文名：初等基數
- 外文名：elementary
初等基數特殊基數的統稱.可數集Acardinal number)三種冪集}(A)的基數2氣一叢的基數}o，可數集A的，以及}(}'o(A))的基數2}統稱初等基數.這三個基數中叭。是自然數集的基數，2九為連續統基數，而2}是實數集上的一切實函式的集合的基數，它們的關係是乒0<2'}}=}<2}".有限基數與初等基數的運算有下列結果:
初等基數
相關詞條
- 初等基數
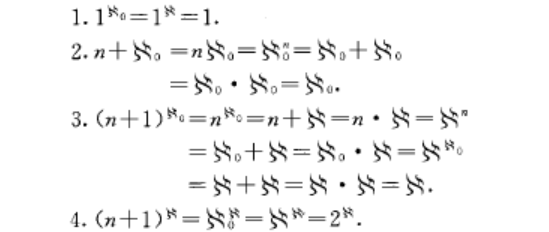
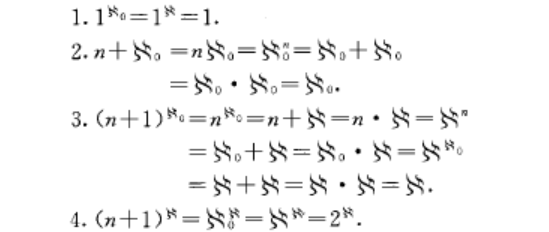
初等基數(elementary特殊基數的統稱。初等基數特殊基數的統稱.可數集Acardinal number)三種冪集}(A)的基數2氣一叢的基數}o，可數集A的，以及}(}'o(A))的基數2}統稱初等基數.這三個基數...
- 初等代數研究(1988年高等教育出版社出版的圖書)
《初等代數研究（上冊）》可供師範院校數學系、科“初等代數研究”課程作為試用教材，也可供中學數學教師參考。目錄 緒言 第一章 自然數 1.1 自然數的基數理論 1.2 自然婁的序數理論 1.3 數學歸納法 習題一 第二章 整數 2.1 整數環 2.2 帶餘除法 2.3 最大公因數與最低公倍數 2.4 素數與合數 2.5...
- 初等代數研究(2022年9月上海社會科學院出版社出版的圖書)
1.2.1基數理論 1.2.2序數理論 1.2.3自然數集的性質 1.2.4自然數的減法與除法 1.2.5數學歸納法 1.3整數環 1.3.1整數概念 1.3.2整數運算與整數環 1.3.3整數集的性質 1.3.4整除和同餘 1.4有理數域 1.4.1有理數的概念 1.4.2有理數的順序 1.4.3有理數的運算 1.4.4有理數集的...
- 初等數學研究(2011年北京大學出版社出版的圖書)
一、自然數的基數理論 二、自然數的序數理論 三、自然數集的一些重要性質 四、擴大的自然數集 第三節 整數集 一、整數的概念與運算 二、整數的順序關係 三、整數集的性質 第四節 有理數集及其性質 一、有理數的運算 二、有理數的順序關係 三、有理數集的性質 第五節 實數集 一、無理數的引入 二、...
- 緊基數
定理3 設κ是正則基數，則下列命題等價：[1]對任意S，S上每一個κ-完全超子可擴充成S上的超濾；[2]對任何 上存在精細的測度；[3]無窮語言 滿足強緊性定理。定理4 若κ≤λ，則下列命題等價：[1]κ是λ-強緊的．[2]存在初等嵌入 ，以κ為臨界點，使得當 時，有 ，滿足 ，[3]若F是集合S...
- 強緊基數
定理3設κ是正則基數，則下列命題等價：[1]對任意S，S上每一個κ-完全超子可擴充成S上的超濾；[2]對任何λ≥κ，Pλ上存在精細的測度；[3]無窮語言 滿足強緊性定理。定理4若κ≤λ，則下列命題等價：[1]κ是λ-強緊的．[2]存在初等嵌入j：V→M，以κ為臨界點，使得當X⊆M，|X| [3]若F是集合...
- 初等國小算術教授本(第一學年下學期用)
第七星期授加大基數於小基數 第八星期授減九八於十一以上數 第九星期授減七以下數於十一以上數 第十星期授減十一以上數於十九以下數 第十一星期授二十之數法寫法及二倍 第十二星期授三倍四倍五倍 第十三星期授六倍及七以上諸倍數 第十四星期授反求倍數 第十五星期授等分 第十六星期本學年總複習 第十七星期續...
- 崗位技能工資制
（一）勞動部負責制定全國性的崗位技能工資制方案和政策；擬訂全國全民所有制大中型企業職工基本工資（崗位技能工資）參考標準；負責協調平衡地區、行業之間有關政策和行業、地區工資關係（包括基本工資總量基數和改革新增基本工資水平等），協調平衡和審批待業、地區工資標準；負責審批少數待業的特殊工資或津貼；負責審核各...
- 萬有模型
假設𝒌為一無窮基數。稱理論T的模型ℳ是𝒌飽和的，如果對一切A⊂M，|A| 齊次模型 [homogeneous mode]假設𝒌為一無窮基數。稱理論T的模型ℳ是T的𝒌齊次模型，如果對於一切A⊂M，|A| 基本嵌入 [elementary embedding]嵌入j：M → N，滿足對一切ℒ公式 和任意 ，均有ℳ⊨ 若且唯若𝒩⊨ ...
- 特殊模型
特殊模型 特殊模型是一個數學術語。特殊模型(special model)一種模型鏈的並.如果一個模型au是一個初等鏈 的並，其中R是基數，每一個令，都是R+飽和的模型，則稱卿是特殊模型.有限模型是特殊模型，飽和模型也是特殊模型.
- 數學名詞
映射 對角 數列 等式 基數 正角 負角 零角 弧度 密位 端點 全集 補集 值域 周期 相位 初相 首項 通項 回數 公比 公差 複數 虛數 實數 實部 虛部 實軸 虛軸 向量 輻角 排列 組合 機率 直線 公理 定義 概念 射線 線段 頂點 始邊 終邊 圓角 平角 銳角 鈍角 直角 ...
- 超越次數
超越次數 超越次數為域論的一個概念。擴域定義 設F為K的擴域，則F在K上的超越次數為F在K上任一超越基的基數。代數定義 設A為域K上的代數。則A的超越次數定義為 其中T為有限的，而且代數無關。性質 1.設A為域K上的代數。則 2.設A為仿射代數，則 ...
- 公理集合論導引(1991年科學出版社出版的圖書)
§5 基數的初等運算 §6 萊文海姆-斯科倫定理 §7 蔻尼定理 §8 不可達基數 習題 第六章 公理與邏輯 §1 公理方法 §2 ZF形式語言 §3 ZF公理系統 §4 邏輯演算 §5 證明與定理 §6 協調性與可滿足性 §7 完全性定理 §8 系統Z與替換公理 §9 正則公理 §10 ZFC的有窮子系統 §11 形式推演 §...
- 數學小百科
03013基數 03014數系 03015自然數 03016整數 03017有理數 03018實數 03019複數 03020組合數學 04021圖論 04022圖 04023樹 04024有向圖 04025中國郵遞員問題 04026旅行推銷員問題 04027四色問題 05028算術 06029代數學 06030多項式 06031代數方程 06032線性代數 06033矩陣 06034行列式 06035線性方程組 06036線性空間 06037...
- 拓樸空間論
2．基數，序數 3．歸納法，良序定理，Zorn引理 第一章 拓撲空間 4．拓撲的導入 5．度量空間 6．相對拓撲 7．初等用語 8．分離公理 9．連續映射 10．連通性 習題 第二章 積空間 11．積拓撲 12．嵌入平行體空間 13．Michael直線 14．0維空間 習題 第三章 仿緊空間 15．正規列 16．局部有限性和可數仿緊...
- 極大線性無關組
它們所含的向量個數（基數）相同。V的子集S的極大線性無關組所含向量的個數（基數），稱為S的秩。只含零向量的子集的秩是零。V的任一子集都與它的極大線性無關組等價。特別地，當S等於V且V是有限維線性空間時，S的秩就是V的維數。定義 設有向量組 ： ，若 中能選出r個向量 ，滿足:(1)向量組 ...
- 亨森引理
亨森引理（Henson lemma）是關於模型同構的一個引理，其可判定初等價結構是否同構。簡介 亨森引理是關於模型同構的一個引理。該引理斷言：對於每個其常量及關係個數少於card⁺(X)（card⁺(X)是card(X)的後繼基數）的一階語言L，若A與B是L的初等價結構，它的定義域與關係是多擴大*X的內實體，並且card(A)=...
- 代數獨立
便會代數獨立於有理數。現在依然沒有證明出集合{π, e}是否代數獨立於有理數。Nesterenko在1996年證明了{π, eπ, Γ}是代數獨立於有理數的。給定一域擴張L/K，我們可以利用佐恩引理來證明總是存在一L的最大代數獨立子集於K。甚至，所有個最大代數獨立子集都會有相同的基數，稱之為此一域擴張的超越次數。...
- 數理邏輯史
他在1883和1891年的論文中全面發展了無窮基數和無窮序數的理論，利用良序集理論和冪集給出一個比一個大的基數和序數。連續統假設在1878年曾被作為估計提出，1883年他認為此假設是可證的。在後一論文裡他也講到良序定理的重要性。但對這二者他始終沒有給出證明。關於悖論，他曾和D.希爾伯特於1895年通信討論過布拉...
- 一般拓撲學(1982年科學出版社出版的圖書)
子集與余集；並與交 關係 函式 序 代數概念 實數 可數集 基數 序數 笛卡兒乘積 Hausdorff極大原理 第一章 拓撲空間 第二章 Moore-Smith收斂 第三章 乘積空間和商空間 第四章 嵌入和度量化 第五章 緊空間 第六章 一致空間 第七章 函式空間 附錄 初等集論 參考文獻 譯者為本書增添的附錄 參考文獻 索 引 ...
- 希爾伯特主義派
.更嚴格地說，就是關於無窮整體的任何講話或意謂實際上都是沒有意義的.然而，其二，我們還是應該如通常那樣去從事數學活動，即我們做起來就好像無窮整體是存在的那樣.”在此，還應提及形式主義派與現代柏拉圖主義派關於數學實無限性在柏拉圖哲學意義上的實在性的爭論.柏拉圖主義者是承認那種具有任意大基數的超窮集合在...
- 數學美
比如，在歷史上，虛數曾一度被看作是“幻想中的數”、“介於存在和不存在之間的兩棲物”；無窮小量dx曾長期被蒙上神秘的面紗，被英國大主教貝克萊稱為“消失了量的鬼魂”；彭加勒把集合論比喻為“病態數學”，外爾則稱康托爾關於基數的等級是“霧上之霧”；非歐幾何在長達半個世紀的時間內被人稱為“想像的...
- 數學課系
另一個研究的領域為其大小，這個導致了基數和之後對無限的另外一種概念：艾禮富數，它允許無限集合之間的大小可以做有意義的比較。結構 許多如數及函式的集合等數學物件都有著內含的結構。這些物件的結構性質被探討於群、環、體及其他本身即為此物件的抽象系統中。此為抽象代數的領域。在此有一個很重要的概念，即...
- 密碼學與網路安全
9.1.2 素數的基數 9.1.3 素性檢驗 9.1.4 Euler Phi-（歐拉?（n））函式 9.1.5 Fermat（費爾馬）小定理 9.1.6 Euler定理 9.1.7 生成素數 9.2 素性測試 9.2.1 確定性算法 9.2.2 機率算法 9.2.3 推薦的素性檢驗 9.3 因數分解 9.3.1 算術基本定理 9.3.2 因數分解方法 9.3.3 ...
- 離散數學(2015年科學出版社出版的圖書)
3.6集合運算與基數概念的擴展 3.6.1並集、交集的擴展 3.6.2基數概念的擴展 3.7習題 第四章二元關係 4.1基本概念 4.1.1二元關係的定義 4.1.2關係的表示 4.2關係的運算 4.2.1關係的並、交、補、差、對稱差運算 4.2.2關係的複合運算 4.2.3關係的逆運算 4.3關係的性質 4.3.1關係性質的概念 ...
- 斐波那契數列
（2）方法二：待定係數法構造等比數列1（初等代數解法）設常數 ，使得 則 時，有：聯立以上 個式子，得：上式可化簡得：那么：（這是一個以 為首項、以 為末項、為公比的等比數列的各項的和）。， 的解為 ，則 （3）方法三：待定係數法構造等比數列（初等代數解法）設 得 構造方程 解得 所以：由(1)、...
