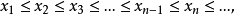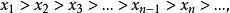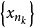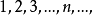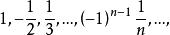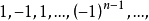序列(sequence)是數學分析的基本概念之一,即可用自然數編號,並按編號從小到大的次序排列的同一類數學對象。若將序列看做集合,它的元素稱為序列的項,但序列並非一般的集合,序列的項有先後次序,並且不同的項可以是相同的元素。序列可以只有有限項,稱為有限序列,不只有限項的序列稱為無窮序列,這是數學分析中通常討論的對象。序列按各項順序排列可寫為a1,a2,…,an,…,簡記為{an}。排在第n位的項an稱為第n項,把n看做在自然數集N中變動時,亦把an稱為通項。序列常隨其所包含的數學對象使用不同名稱,例如:各項都是數的序列稱為數列,各項都是點的稱為點列,各項都是函式的稱為函式列。數列也可看做定義域為自然數集N或其部分Nk={1,2,…,k}的函式或映射(f∶n→an),因此亦稱整序變數。數列還常用數軸上的點列表示,所以數列與直線上的點列可以不加區分。
基本介紹
- 中文名:無窮序列
- 外文名:infinite sequence
- 所屬學科:數學
- 相關概念:序列,函式,有限序列等
- 簡稱:序列
基本介紹
定義1


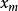

定義2
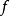
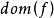
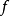
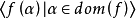
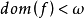
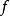
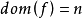
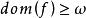

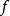
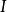

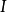
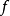



序列的分類與子序列