基本介紹
定義
性質
逆定理
判定方法
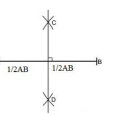
作圖方法
與對稱軸
生活套用

線段垂直平分線一般指本詞條


《線段的垂直平分線》是廣東高州中學國中校區提供的微課課程,主講教師是朱明杏。知識點 1.北師大版/七年級下冊/第五章 生活中的軸對稱/3.簡單的軸對稱圖形 設計思路 從複習軸對稱圖形導入,通過摺疊線段,找出線段的對稱軸,探索線段的垂直平分線的性質,最後讓學生用尺規作圖找出線段的垂直平分線,加強對線段垂...
《線段的垂直平分線的性質》是藥王洞中學提供的微課課程,主講教師為邢雙娜。知識點 國中 數學 1.九.點、線、面、角/1.直線、射線、線段。2.九.點、線、面、角/1.直線、射線、線段/線段中點及其畫法。課程簡介 本屆微課主要是線段的垂直平分線的兩種套用方式,求線段的長度和求角的度數的問題。幫助學生快速...
線段垂直平分線性質的套用 《線段垂直平分線性質的套用》是冶源鎮楊善國中提供的微課課程,主講教師為郭凌雲。教師簡介 郭凌雲於冶源鎮楊善國中任數學老師。知識點 國中 數學 1.十一.三角形/7.特殊三角形/線段垂直平分線的性質 2.十一.三角形/7.特殊三角形/線段垂直平分線的判定 ...
10.利用切線的性質定理:圓的切線垂直於過切點的半徑。除了上述十種主要方法外,還有一些其他方法。例如,利用線段垂直平分線性質的逆定理,即如果一點到線段兩端點的距離相等,那么這一點必在這條線段的垂直平分線上。也可以利用三角函式的計算來證明兩直線垂直。例如,當角a是銳角時,如果sina=1,那么a=90°(當然...
《簡單的軸對稱圖形—線段》是靖邊六中提供的微課課程,主講教師為許新龍 。課程簡介 1.本節通過實踐操作與思考的有機結合,幫助我們認識簡單的軸對稱圖形。經歷探索簡單圖形軸對稱性的過程,進一步體驗軸對稱的特徵,發展空間觀念。 2.探索並了解線段垂直平分線的有關性質。知識點 國中 數學 1.十四.圖形變換/1.軸...
已知線段及所含圓周角作弧是一個數學名詞。已知線段及所含圓周角作弧亦稱已知弦和內接角 作弓形弧,基本作圖題(作圖成法)之一具體表述為:已知線段二及}a,作以二為弦的圓弧AmB ,使} AmB一}a.其具體作法是:1.作線段AB=a及它的垂直平分線MN ;2.過點B作射線BD,使匕ABD =匕a;3.過點B作BD的垂線BE,交...
材料軸對稱指的是組成某個研究物體的材料相對於研究目標周線成軸對稱。相關概念 一、線段垂直平分線的定義:經過線段中點並且垂直於這條線段的直線,叫做線段的垂直平分線。二、圖形軸對稱的性質:如果兩個圖形關於某條直線對稱,那么對稱軸是任何一對對稱點所連線段的垂直平分線.類似地,軸對稱圖形的對稱軸是任何一...
垂直並且平分一條線段的直線稱為這條線段的垂直平分線,或中垂線。線段垂直平分線上的點到線段兩端的距離相等。在軸對稱圖形中,對稱軸兩側的對應點被對稱軸垂直平分。成軸對稱的兩個圖形是全等的。如果兩個圖形關於某條直線對稱,那么對稱軸是任何一對對應點所連線段的垂直平分線。中心對稱圖形 如果一個圖形繞某...
《一個尺規作圖模型》是茂名市祥和中學提供的微課課程,主講老師是楊敏。課程簡介 本節課內容是關於北師大版七年級數學下冊第五章第3節《簡單的軸對稱圖形》的學習與拓展,實現課程的承上啟下作用。主要是讓學生掌握線段的垂直平分線、角平分線的尺規作圖方法。1、解決問題:通過將垂直平分線與角平分線的作圖方法...
1.如果兩個圖形關於某條直線對稱,那么對稱軸是任何一對對應點所連線段的垂直平分線。 2.類似地,軸對稱圖形的對稱軸,是任何一對對應點所連線段的垂直平分線。 3.線段的垂直平分線上的點與這條線段的兩個端點的距離相等。 4.對稱軸是到線段兩端距離相等的點的集合。
泰森多邊形又叫沃洛諾伊圖(Voronoi diagram),得名於Georgy Voronoi,是一組由連線兩鄰點線段的垂直平分線組成的連續多邊形。一個泰森多邊形內的任一點到構成該多邊形的控制點的距離小於到其他多邊形控制點的距離。簡介 泰森多邊形是對空間平面的一種剖分,其特點是多邊形內的任何位置離該多邊形的樣點(如居民點)的...
39.定理 線段垂直平分線上的點和這條線段兩個端點的距離相等 40.逆定理 和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上 41.線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合 42.定理1關於某條直線對稱的兩個圖形是全等形 43.定理2如果兩個圖形關於某直線對稱,那么對稱軸是對應點連線...
中點 定義:把一條線段分為兩條相等線段的點。線上段AC上,若AF=CF,則F為AC中點,反之亦然。定義 把一條線段分為兩條相等的線段的點,叫做這條線段的中點。套用:構造三角形中線 構造三角形中垂線(垂直平分線)構造三角形,梯形中位線
定理 線段垂直平分線上的點和這條線段兩個端點的距離相等 逆定理 和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上 線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合 定理 如果兩個圖形關於某直線對稱,那么對稱軸是對應點連線的垂直平分線 角的性質 對稱性:角具有對稱性,對稱軸是角的角...
39 、定理 :線段垂直平分線上的點和這條線段兩個端點的距離相等 40 、逆定理 :和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上 41 、線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合 42 、定理1 :關於某條直線對稱的兩個圖形是全等形 43 、定理 2 :如果兩個圖形關於某直線對稱...
幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。簡介 “幾何定理”分類 條目 平面幾何:線 平行線判定定理 平行線性質定理 垂直平分線 平行線等分線段定理 平行線分線段成比例定理 角 角平分線定理 角平分線長公式 分角定理 張角定理...
兩條也可,兩線相交確定一點)以線段為例,可以看作是三角形一邊。分別以兩個端點為圓心適當長度(相等)為半徑做圓(只畫出與線段相交的弧即可),再分別以兩交點為圓心,等長為半徑(保證兩圓相交)做圓,過最後的兩個圓的兩個交點做直線,這條直線垂直且平分這條線段即線段的垂直平分線。
39 定理 線段垂直平分線上的點和這條線段兩個端點的距離相等 40 逆定理 和一條線段兩個端點距離相等的點,在這條線段的垂直平分線上 41 線段的垂直平分線可看作和線段兩端點距離相等的所有點的集合 42 定理1 關於某條直線對稱的兩個圖形是全等形 43 定理 2 如果兩個圖形關於某直線對稱,那么對稱軸是對應點...
《義教課程標準實驗教科書(9年級上冊)》是北京師範大學出版社2006年出版的圖書,作者是馬復。內容簡介 《義教課程標準實驗教科書:數學(9年級上冊)(教師教學用書)》內容包括:證明(二);你能證明它們嗎;直角三角形;線段的垂直平分線;角平分線;一元二次方程;花邊有多寬;配方法;公式法;分解因式法;平行...
是線段AB的垂直平分線,則稱點A、B關於直線 互相對稱,點A、B互稱為關於直線 的對稱點,直線 叫做對稱軸。定義一 在平面上,如果圖形F的所有點關於平面上的直線 成軸對稱,直線 叫做圖形下的對稱軸。定義二 在平面上,如果存在一條直線 ,圖形F的所有點關於直線 的對稱點組成的圖形。仍是圖形F自身,則稱圖形...
ΔABC是直角三角形,作AB的垂直平分線n交BC於D ∴ AD=BD(線段垂直平分線上的點到這條線段兩端點的距離相等)以DB為半徑,D為圓心畫弧,與BC在D的另一側交於C'∴DC’=AD=BD∴∠BAD=∠ABD ∠C’AD=∠AC’D (等邊對等角)又∵∠BAD+∠ABD+∠C’AD+∠AC’D =180°(三角形內角和定理)∴∠BAD+...
再認中垂線 《再認中垂線》是山盆中學提供的微課課程,主講教師是周偉。課程簡介 學生對線段的垂直平分線已經有了初步的認識,通過再次來學習線段的垂直平分線的性質,加深對中垂線的認識和了解以及運用。設計思路 由問題來導入新知,引出中垂線的性質,再運用,最後總結。
以F1,F2所在直線為x軸,線段F1F2的垂直平分線為y軸,建立直角坐標系xOy,則F1,F2的坐標分別為(-c,0),(c,0)設M(x,y)為雙曲線上任意一點,根據雙曲線定義知 |MF1-MF2|=2a 即| |=2a 化簡得 因為 所以令 (b>0)得:兩邊除以 得 (a>0,b>0即焦點在x軸上)類似可以得到焦點為F1(0,...
以F1,F2所在直線為x軸,線段F1F2的垂直平分線為y軸,建立直角坐標系xOy,則F1,F2的坐標分別為(-c,0),(c,0)。設M(x,y)為橢圓上任意一點,根據橢圓定義知 |MF₁|+|MF₂|=2a,(a>0)即 將方程兩邊同時平方,化簡得 兩邊再平方,化簡得 又 ,設 ,得 兩邊同除以 ,得 這個形式是橢圓的...
作圖題(construction problem),屬於數學問題的一種類型,是一種先給出一些條件,再求作符合這些條件圖形的題型。作為其他作圖基礎的一些作圖題,稱為基本作圖題.如:1.作一個角等於已知角.2.平分一個已知角.3.經過一點作已知直線的垂線或平行線.4.作線段的垂直平分線.5.分一線段為若干等份.6.已知三邊作三角形...
1.3 線段的垂直平分線(第1課時)線段的垂直平分線(第2課時)1.4 角平分線(第1課時)角平分線(第2課時)一元二次方程 2.1 花邊有多寬 2.2 配方法(第1課時)配方法(第2課時)配方法(第3課時)2.3 公式法 2.4 分解因式法 2.5 為什麼是0.6 18(第1課時)為什麼是0.6 18(第2課時)證明...
到已知線段兩個端點的距離相等的點的軌跡,是這條線段的垂直平分線。到已知角的兩邊距離相等的點的軌跡,是這個角的角平分線。到直線L的距離等於定長D的點的軌跡,是平行於這條直線,並且到這條直線的距離等於定長的兩條直線。到兩條平行線距離相等的點的軌跡,是和這兩條平行線平行且距離相等的一條直線。到兩...
