在一條直線或平面上,另一條直線和已知直線或平面夾角為90度,就是垂直線。 在一條直線上畫一個點離它最近的線,垂直線是最短的。
基本介紹
- 中文名:垂直線
- 外文名:perpendicular line
- 所屬領域:幾何學
- 特點:與另一直線夾角90°的直線
定義
證明的方法
說明


例題解析
 圖1
圖1








 圖2
圖2

解釋證明
說明
例題解析








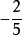










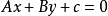








在一條直線或平面上,另一條直線和已知直線或平面夾角為90度,就是垂直線。 在一條直線上畫一個點離它最近的線,垂直線是最短的。


 圖1
圖1








 圖2
圖2









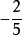










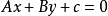







在一條直線或平面上,另一條直線和已知直線或平面夾角為90度,就是垂直線。 在一條直線上畫一個點離它最近的線,垂直線是最短的。...
垂直天線是指與地面垂直放置的天線。它有對稱與不對稱兩種形式,而後者套用較廣。對稱垂直天線常常是中心饋電的。不對稱垂直天線則在天線底端與地面之間饋電,其最大...
垂直線圈法(vertical-loopmethod)是一種半定源裝置的虛分量電磁剖面觀測方法。...... 在觀測過程中,發射線圈被布設在測線之外40~100米的某處,線圈面垂直且對準接...
垂直中線錯覺也稱垂直-水平錯覺(horizontal-vertical illusion),是指兩條等長的直線,一條垂直於另一條的中點,那么垂直線看去比水平線要長一些。...
在EUV光刻中,由於存在陰影效應等,同一線條分別水平與垂直放置時,導致晶圓上水平、垂直的線條寬度存在差別,稱為水平垂直線寬差(HVB)。...
青銅器最簡易的紋飾之一。其狀為若干平行垂直線紋,裝飾於器腹,直線有的較粗,有的較細。通行於商到西周晚期。 ...
在給定的兩個垂直方向上,直線度公差帶是截面尺寸公差值t1×t2的四稜柱內的區域。 稜線必須位於水平方向距離為公差值0.05mm,垂直方向距離為公差值0.03mm的四稜柱...
當兩條直線相交所成的四個角中,有一個角是直角時,即兩條直線互相垂直,其中一條直線叫做另一直線的垂線,交點叫垂足。垂線段是一個圖形,點到直線的距離是一個...
治癢穴是在手腕放下時,從肩膀凹窪,以垂直線而下,該線與乳頭的水平線相交處。 指壓此穴,對於治療濕疹等騷癢類疾病很有療效。 定位...
分份線是在分出的區域內再細分出發片形成精確修剪的層次。...... 1水平線:又稱“—”字線,可使髮型輪廓平行,重量感強。2垂直線:又稱豎直線,可使髮型輪廓移動...
格子線是在型線圖中,由基線、水線、站線、縱剖線、中心線、半寬框線線等水平線和垂直線組成的矩形格子。...
在光的傳播方向上,光矢量只沿一個固定的方向振動,這種光稱為平面偏振光,由於光矢量端點的軌跡為一直線,又叫做線偏振光。光矢量的方向和光的傳播方向所構成的平面...
超五類/D級水平與垂直布線; 適用於有電磁干擾以及對數據安全性要求較高的環境; 高傳輸速率網路套用:千兆乙太網,10/100BaseT等。...
具體操作方法是:用一條沾了墨的線,兩個人每人拿一端然後彈在地上或者牆上。作用是用來確定水平線或者垂直線,又或者作為砌牆的參考線;另外在工地裡面找水平位置的...
投線儀,或稱墨線儀,一般指可發出垂直或水平的可見雷射,用於在目標面上標註水平線或垂直線。...
