泰森多邊形又叫馮洛諾伊圖(Voronoi diagram),得名於Georgy Voronoi,是由一組由連線兩鄰點線段的垂直平分線組成的連續多邊形組成。一個泰森多邊形內的任一點到構成該多邊形的控制點的距離小於到其他多邊形控制點的距離。
基本介紹
- 中文名:泰森多邊形
- 外文名:Thiessen Polygon
- 性質:多邊形
- 泰森多邊形內:的點到相應離散點的距離最近
- 美國氣候學家:A·H·Thiessen
簡介,數學描述,建立步驟,特徵,泰森多邊形面積,作用,
簡介
泰森多邊形是對空間平面的一種剖分,其特點是多邊形內的任何位置離該多邊形的樣點(如居民點)的距離最近,離相鄰多邊形內樣點的距離遠,且每個多邊形內含且僅包含一個樣點。由於泰森多邊形在空間剖分上的等分性特徵,因此可用於解決最近點、最小封閉圓等問題,以及許多空間分析問題,如鄰接、接近度和可達性分析等。
數學描述
設平面區域B上有一組離散點 (i = 1,2,3,…,k ,k為離散點點數),若將區域B用一組直線段分成k個互相鄰接的多邊形,使得:
(i = 1,2,3,…,k ,k為離散點點數),若將區域B用一組直線段分成k個互相鄰接的多邊形,使得:

(1)每個多邊形內含有且僅含有一個離散點;
(2)若區域B 上任意一點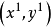 位於含離散點
位於含離散點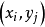 的多邊形內,不等式
的多邊形內,不等式 (1)
(1)
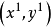
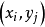

在 時恆成立;
時恆成立;

(3)若點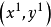 位於含離散點
位於含離散點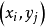 的兩個多邊形的公共邊上,則等式
的兩個多邊形的公共邊上,則等式 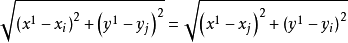 (2)
(2)
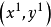
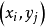
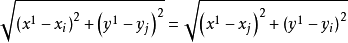
成立。
由此得到的多邊形叫泰森多邊形。用直線連線每兩個相鄰多邊形內的離散點形成的三角形叫泰森三角形。
建立步驟
泰森多邊形的建立:
建立泰森多邊形算法的關鍵是對離散數據點合理地連成三角網,即構建Delaunay三角網。建立泰森多邊形的步驟為:
3、對與每個離散點相鄰的三角形按順時針或逆時針方向排序,以便下一步連線生成泰森多邊形。設離散點為o。找出以o為頂點的一個三角形,設為A;取三角形A除o以外的另一頂點,設為a,則另一個頂點也可找出,即為f;則下一個三角形必然是以of為邊的,即為三角形F;三角形F的另一頂點為e,則下一三角形是以oe為邊的;如此重複進行,直到回到oa邊。
特徵
1、每個泰森多邊形內僅含有一個離散點數據;
2、泰森多邊形內的點到相應離散點的距離最近;
3、位於泰森多邊形邊上的點到其兩邊的離散點的距離相等。
泰森多邊形面積
由於泰森多邊形面積隨點集的分布而發生變化,因此可用多邊形面積的變異係數CV值(即泰森多邊形面積的標準差與平均值的比)來衡量凸多邊形面積的變化程度,從而評估樣點的分布類型。
CV值公式見式(1)、式(2):
式(1):


式(2):
CV=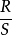
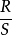
式中,Si是第i個多邊形的面積,S為多邊形面積的平均值,n是多邊形面積的個數,R為方差.當點集分布類型為“均勻”時,多邊形面積變化小,CV值就小,當點集為“集群”分布時,集群內的多邊形面積較小,而集群間的多邊形面積較大,CV值也大.Duyckaert提出了三個建議值:當點集為“隨機分布”時,CV=57 %(包括33%.--64% ) ;當點集為“集群”分布時,CV=92%(包括>64% );當點集為“均勻分布”時,CV=29%(包括<<33% )。要注意的是,位於邊緣上的點的泰森多邊形面積直接受到人為劃定邊界的影響,邊界越大,邊緣點的泰森多邊形面積也越大,反之邊緣點的泰森多邊形面積越小,所以在計算泰森多邊形面積的CV值時,要考慮邊界的影響。

