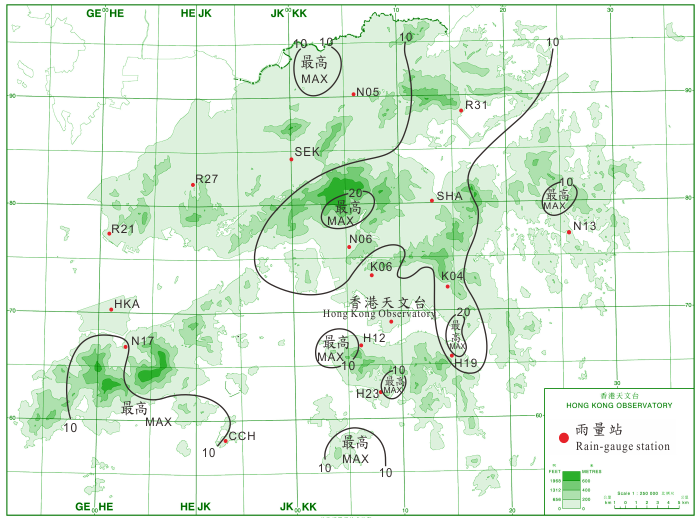
等雨量線是圖上表示某一給定時間內(如年、季、月)的雨量相等各點的連線。可顯示雨量的地理分布狀況。
基本介紹
- 中文名:等雨量線
- 外文名:isohyet
定義,研究意義,面雨量計算方法,算術平均法,泰森多邊形法,等雨量線法,
定義
研究意義
面雨量是水文學的一個重要參量,面雨量的估算直接關係到洪水預報精度和洪水調度決策的科學性。由於降雨的地點、強度、持續時間等因素的隨機性以及流域下墊面地貌特徵的不均勻分布,怎樣在有限降水資料的基礎上,結合影響降水的因素,儘量精確地計算區域的面雨量一直是研究的熱點和重點。面雨量客觀計算方法有等雨量線法、面積權重法、泰森多邊形法、客觀運行法和站點平均計算等。其中,傳統和最為精確的計算方法是等雨量線法。
面雨量計算方法
算術平均法
將流域內各雨量站同期降雨量觀測資料取其總和再除以測站數,即為流域平均雨量。該法忽略各雨量站所能代表的流域面積範圍,認為各站具有相同面積權重和高程權重,因而可以取其算術平均值。
當流域內雨量站分布較為均勻,地形變化不大的情況,用算術平均法計算流域平均雨量,可獲得較為合理的成果。當流域內雨鼠站稀少,而流域四周的自然地理及氣候特徵與研究流域基本相似時,也可將其四周雨量站的同期觀測資料加入計算,但是外圍的雨量站必須形成一圈,而且站間的間隙應基本接近。算術平均法因其未能考慮到降雨量的實際分布特性,因此,它所算得的成果,只能粗略代表流域平均雨量的真值,但因該法計算簡便,工作量較小,目前被廣泛使用。
泰森多邊形法
該法粗略地考慮了降雨量在地區上分布的不均勻性,根據站點的布設為每個雨量站劃定了一塊相對合理的面積。因此,雨量站布設的密度,將直接影響到成果的可靠程度。所以只要測站位置確定,各站的面積權重為常數,故此法為固定權重法。但採用的雨量站數發生變化時,泰森多邊形隨之變化,各站的面積權重亦發生變化,因此,在計算中若需增加或減少雨量站數目,必須重新繪製和量算各站控制面積。
等雨量線法
具體計算方法是根據繪製的等雨量線圖,求出各相鄰等雨量線之間的面積,然後乘上各相鄰雨量線雨深的平均值,即為該面積的降水總量,再將各面積上的降水總量相加,除以全流域面積,即得流域面雨量,公式如下:
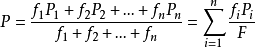
式中:P為平均面雨量,f1,f2...fn為相鄰等雨量線間的面積,P1,P2...Pn為相鄰等雨量線間雨深平均值,F為流域總面積。
可以看出,該法是不等權重法,可以更完善地說明地形、地而高程變化及其它影響因素對降雨址空間分布的影響,因此,該法比前述各種方法能更完養地利用所有的雨最站資料。但繪製等雨量線要求有足夠數量的雨量觀測資料,只有較大流找雨量站數量較多時,才有條件使用此法。