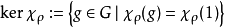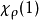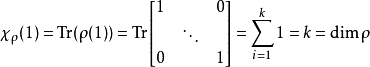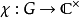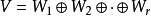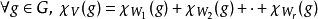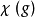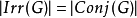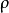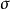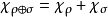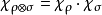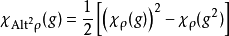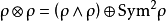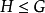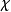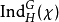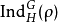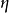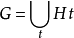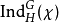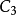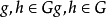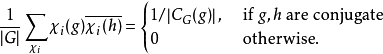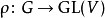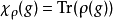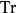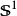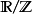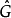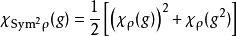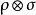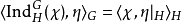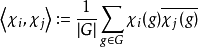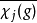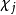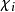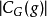特徵標理論

在數學裡，尤其是在群表示理論里，一個群表示的特徵標（character）是指一個將群的每個元素連結至表示空間這個域內的每個元素之函式。特徵標蘊藏著群的許多重要性質，且因此可以用來做群的研究。特徵標理論是對有限簡單群分類的一個有重要的工具。

基本介紹

• 中文名：特徵標理論
• 分類：群表示論
• 套用：數理科學

定義

設V為一個域F上的有限維向量空間且設 為一個群G於V上的表示。則ρ的特徵標即為如下給定之函式：

其中 為矩陣的跡數。

一個特徵標χρ若被稱為是不可約的，即表示ρ是一個不可約表示。若被稱為是線性的，則表示ρ的維度等於1。χρ的核為集合

其中 是χρ在群單位元上的值。當ρ是G的k維表示且1為G的單位元時，

和特徵標群的情況不同，一個群的特徵標通常不會自己“形成”一個群。

拓撲群的情形

在調和分析中，通常定義局部緊阿貝爾拓撲群G的特徵標為連續群同態 ；在此， 表示單位圓構成的群，等價地說就是 。

部分作者將特徵標的定義放寬為連續群同態 ，而將取值在 則稱作么特徵標。其他人則保留原初定義，而將這類廣義的特徵標稱為擬特徵標。

G 的全體特徵標構成一個群 ，群二元運算的定義是 ，稱為對偶群。龐特里雅金對偶性總結了對偶群的一般性質。

性質

1、特徵標是一個類函式，即為對一個共軛類內的所有元素來說，χ會是個常數。

2、兩個同構的表示會有相同的特徵標。若係數域的特徵char(F)=0，則兩個表示為同構的，若且唯若它們有著完全相同的特徵標。

3、若一個表示可以是多個子表示的直和： ，則其相對應的特徵標會是其所有子表示的特徵標之和：

4、在有限群的情況下，每個特徵標 都是n個m次單位根之和，其中n為表示內域的維度，m則是g的階。

5、若F是代數封閉的且char(F)不可以整除G的階|，則G的不可約特徵標之數量等於G的共軛類數： 。

算術性質

令 和 為G的兩個表示，則有下列的等式成立：

其中 為兩者的直和， 為兩者的張量積， 為 的共軛轉置，以及Alt稱為交替積 而Sym則稱為對稱方，其值由下式決定：

特徵標的誘導與限制

設G 為有限群， 為其子群，而 為 G 的表示，其特徵標記為 。令 為誘導表示 的特徵標；根據弗羅貝尼烏斯互反定理，對所有 G 的特徵標 ，恆有下述等式

此等式可用來刻劃類函式 。事實上，若選定陪集分解

還可以明確地寫下 的取值：

特徵標表

一個有限群的不可約特徵標可以形成一個特徵標表，其蘊含著許多有關群G在緊緻形式時的有用資訊。每一行標記著一個不可約特徵標且包含著此一特徵標在每個G的共軛類上的值。

下面是有三個元素之循環群 的特徵標表：

其中的u為一個原三次單位根。特徵標表總會是正方的，因為不可約表示的數目總會相等於共軛類的數目。特徵標表的第一個行總會是1，其對應至群的當然表示上。

正交關係

有關特徵標表最重要的性質之一為其在行與列上都會有著正交關係。對特徵標(即對特徵標表中的行)的內積由下給出：

其中， 表示 在g上的值的複數共軛。

對於此一內積而言，不可約特徵標兩兩正規正交：

對表中的列的正交關係則由下列給出：

對 ，其和為

其中相加的範圍為所有G的不可約特徵標，而符號則表示為g的共軛類之大小。

此一正交關係可以幫助許多的運算，如：

• 將一個未知特徵標分解成不可約特徵標的線性組合。
  
• 當只有一些不可約特徵標為可知時，建構其完整的特徵標表。
  
• 求出群的共軛類的表示的中心化子的階。
  
• 求出群的階。
  

特徵標表性質

一個群G的某些性質可以由其特徵表中推導出來：

1、G的階就是表上所有特徵標之在1上的取值的平方：(χ(1))2的總和（伯恩賽德公式）。

2、G是可換的若且唯若對每個在表上的特徵標，χ(1) = 1。

3、G有一個非當然正規子群(即G不是一個簡單群)若且唯若對於某些表上的非當然特徵標χ和一些於G內的非單位元素g，會有χ(1) = χ(g)。

特徵標表通常不會將群分至同構：例如，四元群Q和有8個元素的二面體群D4會有同樣的特徵標表。對有限群之特別例子，詳見有限群表示理論。一維表示的特徵標會形成一個特徵標群，其和數論中有著很重要的關連。