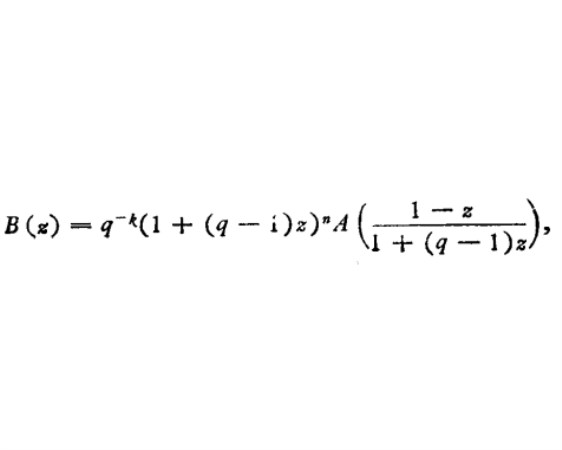麥克威廉斯定理

麥克威廉斯定理(MacWilliams theorem)是關於編碼理論中的一個重要結論，它給出了線性碼C與它的對偶碼C^⊥的重量計數子之間的相互聯繫，這個定理由麥克威廉斯(F.J.MacWilliams)於1962年得到，范·林特(J.H.van Lint)於1971年利用特徵標理論給出了該定理的一個簡潔證明，若C^⊥的重量計數子已知，則該定理給出了關於n+1個未知數A₀，A₁，…，A_n的n+1個方程的線性方程組，從而可解方程組求得線性碼C的重量計數子。

基本介紹

• 中文名：麥克威廉斯定理
• 外文名：MacWilliams theorem
• 所屬學科：數學（組合設計）
• 簡介：關於編碼理論中的一個重要結論
• 提出者：麥克威廉斯(F.J.MacWilliams)

基本介紹

編碼理論中一個最基本的結論是屬於F.J.MacWiUiams(1963)的，它給出了一個線性碼的重量計數子與其對偶碼的重量計數子之間的關係。

定理設C是F_q上一個[n，q]碼，重量計數子為A(z)，又設B(z)是C^⊥的重量計數子，那么

麥克威廉斯定理的證明

設是(F_q，+)的任意一個非平凡特徵標。令，我們定義

則

若v∈C^⊥，則內和是|C|，若v∉C^⊥，則內和<u，v>取到F_q中每個值的次數相同，即內和為0。所以

把重量函式推廣到F_q上：若v=0，則記w(v)=0，否則記w(v)=1。那么令u=，v=後，我們由g(u)的定義得

在最後的表達式中，內和當u_i=0時等於1+(q-1)z，當u_i≠0時等於

因此

由於，把（2）代入（1）即得定理。