以線性分組碼的一致校驗矩陣為生成矩陣產生的線性分組碼成為原線性分組碼對偶編碼。是研究線性碼的一種工具,是從一個碼派生出的另一個碼。
基本介紹
- 中文名:對偶碼
- 外文名:dual code
- 屬性:研究線性碼的一種工具
定義,實例,
定義
在Fnq中定義兩個向量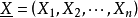 與
與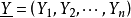 的內積為
的內積為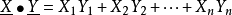 。當
。當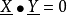 時,稱
時,稱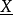 與
與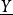 正交,與Fnq中線性碼C的每一個碼字正交的向量
正交,與Fnq中線性碼C的每一個碼字正交的向量 的集合,稱為C的對偶碼,記為C〦,當C為[n,k]線性碼時,C〦為[n,n-k]線性碼;當C為循環碼時,C〦也是循環碼;當C為MDS碼時,C〦也是MDS碼。因此,對偶碼這一概念有助於線性碼性質的研究,麥克威廉斯(MacWilliams,F.J.)揭示了線性碼與它的對偶碼的重量計數子之間的聯繫,從而有助於計算線性碼的重量計數子。
的集合,稱為C的對偶碼,記為C〦,當C為[n,k]線性碼時,C〦為[n,n-k]線性碼;當C為循環碼時,C〦也是循環碼;當C為MDS碼時,C〦也是MDS碼。因此,對偶碼這一概念有助於線性碼性質的研究,麥克威廉斯(MacWilliams,F.J.)揭示了線性碼與它的對偶碼的重量計數子之間的聯繫,從而有助於計算線性碼的重量計數子。
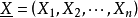
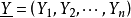
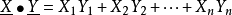
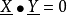
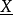
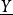

實例
Hamming(7,4)碼的生成矩陣G和H:
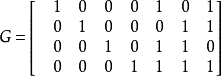
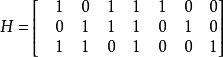

以H作為生成矩陣的(7,3)碼,不過和(7,4)碼不同,信息位在後面三位。
G生成的(7,4)碼的24=16個碼字:
(0000000) (0001111) (0010110) (0011001)
(0100011) (0101100) (0110101) (0111010)
(1000101) (1001010) (1010011) (1011100)
(1100110) (1101101) (1110000) (1111111)
這16個碼字是4位信息m={0000,0001,0010,0011,0100,0101,0111,1000,1001,1010,1011,1100,1101,1110,1111}分別作m●G的結果。

