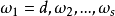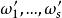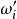阿斯莫斯一馬特森定理

基本介紹

若C為q元[n，k，d]線性碼，若存在整數t(0<t<d)，使得對偶碼C^⊥中至多有d-t個非零重量ω適合1≤ω≤n-t，則C中重量d的碼字的支撐集全體構成集{1，2，…，n}上的一個t設計，當q=2時，C中任一重量τ的碼字的支撐集全體構成t設計。

下面以擴充戈萊碼為例說明這一定理的套用，設U為一個11階方陣，其(i，i+1)位置為1，其餘的元素為0，記

A=I+U+U³+U⁴+U⁵+U⁹，

其中I為單位陣，以E及Φ分別記元素全為1及全為0的行向量，若

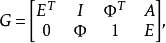
則以G為生成矩陣的二元[24，12]線性碼稱為擴充戈萊碼。這是一個雙偶自對偶碼，其重量計數子為

A(z)=1+759z⁸+2576z¹²+759z¹⁶+z²⁴.

由阿斯莫斯-馬特森定理得到：重量8的碼字構成一個施泰納系S(5，8，24)；而重量12及16的碼字分別構成5-(24，12，48)設計及5-(24，16，78)設計。

Assmus-Mattson定理有一個針對線性碼或者非線性碼的推廣。考慮到(n,M,d)碼C(可能非線性)的距離分布為序列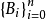

, B_i為距離為i的碼字對的數目,該數目可以整除M。非線性對偶碼的距離分布可以由MacWiliams變換表示,具體為下述等式:

如果C為線性的,則

為對偶碼C^⊥的分布。

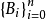
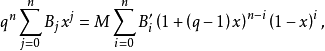
令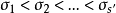

為使B'_i≠0的非零下標i,則d'=σ₁稱為C的對偶距離,s’為C的擴展距離。

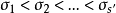
定理1 (n,M,d)碼C含有0向量且距離分布為序列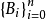

,s為該碼字非零距離數。當B_n=0時,令

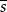=s;當B_n>0時,令

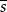=s-1。

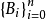
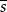
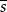
(a)如果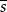

<d ,則碼C中任何重ω≥d'-s的碼字形成(d'-

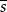)-設計；

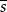
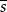
(b)如果d-s'≤s'<d，則任何固定重量的碼字形成(d-s')-設計。

定理2 如果C為二元偶自對偶碼, (包括僅具有自對偶形式的碼) ,其長度為n=2(mod8),則C∪C^⊥中具有固定重量的碼字形成3-設計。

定理3 C為二元[4n+2,k ]碼,其所有的碼字重量為偶數，則其重量為2n和+2的碼字形成互補的t-設計。

定理4 C內二元[n,k,d ]碼,具有非零碼字重量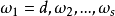

,令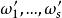

為其對偶碼的非零重量，t為滿足0<t<d的最大整數, 則最多有d-t個重量

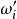滿足,0<w'_i≤n-t。如果w_2≥d +4,則或者C中非零重量カw_i的碼字形成t設計,或者所有的最小重量碼字形成{1,000,t,+21}設計。