基本介紹
- 中文名:殘差平方和
- 外文名:residual sum of squares/sum squared residual
- 簡稱:SSE
- 所屬學科:數理科學
- 用途:衡量模型擬合程度
公式概念
計算
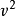
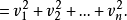
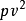
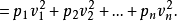
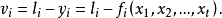
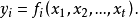
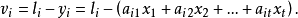
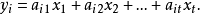
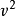
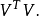

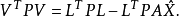
性質
分布
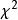
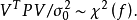
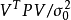
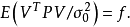
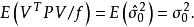
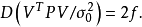
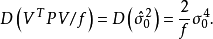
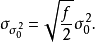
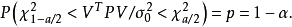
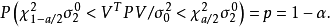
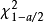
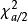
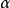
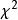

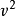
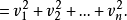
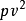
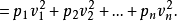
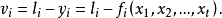
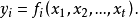
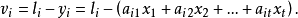
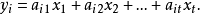
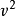
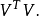

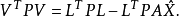
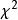
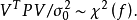
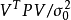
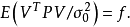
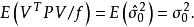
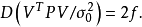
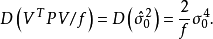
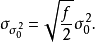
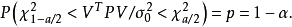
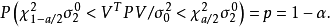
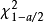
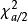
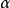
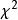
殘差平方和是線上性模型中衡量模型擬合程度的一個量,用連續曲線近似地刻畫或比擬平面上離散點組,以表示坐標之間函式關係的一種數據處理方法。用解析表達式逼近離散...
剩餘平方和是統計學術語,也稱作殘差平方和,是實際值與估計值之差的平方的總和,也就是誤差項平方的總和,利用剩餘平方和可以很好地表示剩餘的總和。...
誤差平方和又稱殘差平方和、組內平方和等,根據n個觀察值擬合適當的模型後,餘下未能擬合部份(ei=yi一y平均)稱為殘差,其中y平均表示n個觀察值的平均值,所有n個...
,這部分的值就小,模型不合適,這部分的值就大,稱為失擬誤差,對應的殘差平方和由兩部分構成,一部分是純誤差平方和,另一部分是擬合不佳所引起的擬合誤差平方和。...
反覆殘差法將模型線性化的一種疊代算法,由Subba Rao在處理雙線性模型時提出。 Subba Rao提出了反覆殘差法估算模型參數,該法是在假定模型階數、模型參數初值和計算...
越小,即模型的擬合效果越好;R2越小,殘差平方和越大,即模型的擬合效果越差。線上性回歸模型中,R2表示解釋變數對於預報變數變化的貢獻率。R2越接近於1,表示回歸的...
其中:SST=SSR+SSE,SST (total sum of squares)為總平方和,SSR (regression sum of squares)為回歸平方和,SSE (error sum of squares) 為殘差平方和。...
為假定後k個係數為零時(即少了k個自變數)的模型的殘差平方和。用F檢驗有許多優良性,在這方面,中國統計學家許寶騄早期做了許多工作,後來美籍羅馬尼亞數學家瓦爾德...
最小二乘法(又稱最小平方法)是一種數學最佳化技術。它通過最小化誤差的平方和尋找數據的最佳函式匹配。利用最小二乘法可以簡便地求得未知的數據,並使得這些求得...
判定係數(coefficient of determination),也叫可決係數或決定係數,是指線上性回歸中,回歸平方和與總離差平方和之比值,其數值等於相關係數的平方。它是對估計的回歸...
其中 是誤差平方和(殘差平方和)。估計值和實際值之間的關係是:其中 服從卡方分布,自由度是 。對普通方程的解可以為:這表示估計項是因變數的線性組合。進一步地...
線上性回歸中引入新自變數後,所減少的殘差平方和與該自變數引入前的殘差平方和之比稱為因變數與新引入的自變數之間的偏判定係數,其數值等於相應樣本偏相關係數的平方...
剩餘標準差SE,也稱均方差,統計學概念,線上性回歸分析中,真實值和估計值之間的差稱為殘差(或者剩餘量),所有預測值的殘差平方和(或者剩餘平方和),剩餘標準差就是...
復判定係數及R2=1-SSE/SST(其中SSE為殘差平方和,SST為總平方和)是用來說明因變數的變動中可以用自變數來解釋的比例。它可以反映模型的好壞,但由於隨著自變數的...
為檢驗兩個變 量之間的線性關係是否顯著,需要構造用於檢驗的統計量。該統計量的構造是以回歸平方和(SSR)和殘差平方和(SSE)為基礎的。 [1] ...
(1) 殘差平方和縮小與決定係數增大。如果引人一個自變數後模型的殘差平方和減少很多,那么說明該自變數對因變數y貢獻大,將其引入模型;反之,說明該自變數對因變數y...
式中Q為殘差平方和,U為回歸平方和,N為樣本數,K為變數數,檢驗不顯著時要修改模型。 路徑分析是多元回歸分析的延伸,與後者不同的是:①路徑分析間的因果關係是...
方差分析表(analysis of variance table)是指為了便於進行數據分析和統計判斷,按照方差分析的過程,將有關步驟的計算數據,例如差異來源、離差平方和、自由度、均方和...
有許多衡量擬合優度的標準,最常用的一種做法是選擇參數c使得擬合模型與實際觀測值在各點的殘差(或離差)ek=yk-f(xk,c)的加權平方和達到最小,此時所求曲線稱作...
(2)做一個含有滯後項x的回歸,即在前面的回歸式中加進滯後項x,這是一個無約束的回歸,由此回歸得到無約束的殘差平方和RSSUR。(3)零假設是H0:α1=α2=…=...
3 損失函式:“非線性回歸”對話框是對整個因變數的運算法則,但是,損失函式是對某一個統計量的運算法則,spss默認是使用最小殘差平方和找出非線性模型,也可以自己...
上面因果關係的最後一種表達方法已經接近我們最常用的格蘭傑因果檢驗方法,統計上通常用殘差平方和來表示預測誤差,於是常常用X和Y建立回歸方程,通過假設檢驗的方法(F...
sst離差平方 離差平方和(SST)=回歸平方和(SSR)+殘差平方和(SSE) sst智慧型安保 Smart and Secure Trade lines,SST 華盛頓安全技術策略委員會推出的。SST其實是...
具體到,L=-(n/2)*ln(2*pi)-(n/2)*ln(sse/n)-n/2.其中n為樣本量,sse為殘差平方和表明增加自由參數的數目提高了擬合的優良性,AIC鼓勵數據擬合的優良性...
