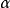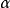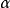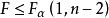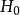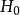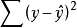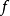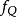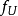剩餘平方和是統計學術語,也稱作殘差平方和,是實際值與估計值之差的平方的總和,也就是誤差項平方的總和,利用剩餘平方和可以很好地表示剩餘的總和。
基本介紹
- 中文名:剩餘平方和
- 外文名:residual sum of square
- 別名:離差平方和
- 屬性:統計學術語
- 相關概念:線性回歸、總離差平方和等
定義,相關介紹,
定義
相關介紹
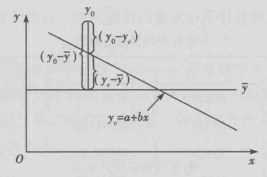 圖1 離差分解示意圖
圖1 離差分解示意圖回歸分析表明,因變數y的實際值(觀察值)有大有小、上下波動,對每一個觀察值來說,波動的大小可用離差(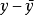 )來表示。離差產生的原因有兩個方面:一是受自變數
)來表示。離差產生的原因有兩個方面:一是受自變數 變動的影響;二是受其他因素的影響(包括觀察或實驗中產生的誤差的影響)。n個觀察值總的波動大小用總離差平方和
變動的影響;二是受其他因素的影響(包括觀察或實驗中產生的誤差的影響)。n個觀察值總的波動大小用總離差平方和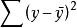 表示。
表示。
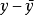

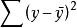
由圖1可以看出,每個觀察點的離差可以分解為兩部分,即
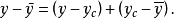
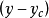
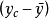
將上式兩邊平方,然後對所有的n求和,則有
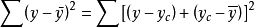
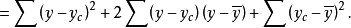
式中,交錯的乘積項等於零,因而總離差平方和為
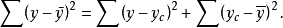
剩餘平方和又稱殘差平方和,它反映了自變數 對因變數
對因變數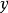 的線性影響之外的一切因素(包括
的線性影響之外的一切因素(包括 對
對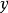 的非線性影響和測量誤差等)對因變數
的非線性影響和測量誤差等)對因變數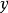 的作用。回歸平方和表示在總離差平方和中,由於
的作用。回歸平方和表示在總離差平方和中,由於 與
與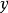 的線性關係而引起因變數
的線性關係而引起因變數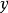 變化的部分。
變化的部分。

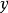

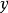
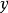

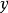
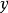
上式可寫成
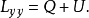
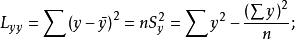
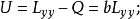
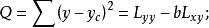
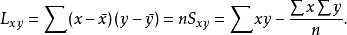
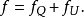
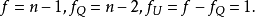
在總離差平方和 中,Q越大就意味著U越小,U越小表示變數間線性相關性越低,若且唯若b=0時,U是最小的。可見,要檢驗總體兩變數間是否真正線性相關,可以檢驗總體回歸係數b是否等於零。
中,Q越大就意味著U越小,U越小表示變數間線性相關性越低,若且唯若b=0時,U是最小的。可見,要檢驗總體兩變數間是否真正線性相關,可以檢驗總體回歸係數b是否等於零。

①提出零假設和備擇假設:
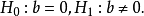
②當x與y有線性關係時,可以用F統計量檢驗零假設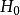 。
。
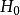
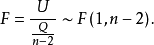
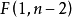
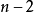
這時,若給定顯著性水平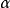 ,計算F值與查表得到的F值比較(
,計算F值與查表得到的F值比較(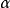 一般取0.05,0.01等,1-
一般取0.05,0.01等,1-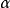 表示檢驗的可靠度)。如果
表示檢驗的可靠度)。如果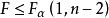 ,則稱變數x與y沒有明顯的線性關係,接受
,則稱變數x與y沒有明顯的線性關係,接受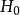 ,說明回歸方程不顯著;如果
,說明回歸方程不顯著;如果 ,則拒絕
,則拒絕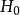 ,說明x與y有顯著的線性關係。
,說明x與y有顯著的線性關係。