基本介紹
- 中文名:無偏估計
- 外文名:unbiased estimate
- 套用學科:統計學
- 相應概念:無偏性
- 包含:無偏估計、漸近無偏估計
- 套用:測驗分數統計
定義
無偏估計








有偏估計







優良性
沒有系統偏差


解釋



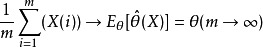



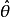

性質





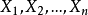































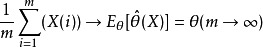



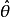






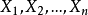










無偏估計是用樣本統計量來估計總體參數時的一種無偏推斷。估計量的數學期望等於被估計參數的真實值,則稱此估計量為被估計參數的無偏估計,即具有無偏性,是一種...
但在大量重複抽樣時,所得到的估計值平均起來應與待估參數的真值相同,換句話說,希望估計量的均值(數學期望)應等於未知參數的真值,這就是所謂無偏性(Unbiasedness...
漸近無偏估計量(asymptotic unbiased estimator)是指當樣本容量n 無限增大時,近似無偏的估計量。...
無偏估計值,樣本估計量的期望值等於真實值 。...... 如算術平均值X是μ的無偏估計值,樣本方差S2是σ2的無偏估計值。但最大似然估計值σ′2不是σ2的無偏...
漸近有效無偏估計是一種參數估計方法.它是對隨機向量的聯合機率密度函式中未知參數的一種估計...
亦稱近似無偏估計。 ...... 亦稱近似無偏估計。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995年03月第1版,第126頁 V百科往期回顧 詞條統計 瀏...
統計學上, 最小方差無偏估計(minimum-variance unbiased estimator,簡寫為MVUE)是一個對於所有無偏估計中,擁有最小方差的無偏估計。若無論真實參數值θ是多少,最...
若g(θ)的無偏估計量T0(X1,X2,...,Xn)對g(θ)的任意無偏估計量T(X1,X2,...,Xn)都有Var[T0]≤Var[T],則稱T0為g(θ)的一致最小方差無偏估計...
無偏性的含義是:由於未知參數的估計量是一個隨機變數,對於不同的樣本它有不同的估計量.這些估計量對於參數的真實取值,一般都會有偏差,要求不出現偏差幾乎是不可能...
最小方差無偏估計量(minimum varianceunbiased estimator) 未知參數0的一切無偏估計中方差最小的估計量。例如,對於正態總體N(μ,o2),其簡單隨機樣本的均值x-藝x...
在統計學中,估計誤差是此估計量的期望值與估計參數的真值之差。誤差為零的估計量或決策規則稱為無偏的。否則該估計量是有偏的。在統計中,“誤差”是一個函式...
如果一個參數的估計量具有線性(估計量是樣本觀察值的線性函式)、無偏(估計量的數學期望等於真值)和估計誤差方差最小等統計學性質,稱其為最佳線性無偏估計量。 應...
當估計值的數學期望等於參數真值時,參數估計就是無偏估計。當估計值是數據的線性函式時,參數估計就是線性估計。當估計值的均方差最小時,參數估計為一致最小均方...
)不存在偏倚。無偏樣本使統計數據免受系統誤差的影響。在此意義下,無偏樣本與無偏估計的概念不同。 [1] 參考資料 1. 鄭家亨,統計大辭典,中國統計出版社,1995...
最佳無偏估計量(值)best unbiased estimator多個不同的無偏估計量中方差最小的無偏枯計量。 ...
數學期望恰好等於被估計未知參數真值的估計量稱為無偏估計量。若未知參數θ的估計量與給定的統計量滿足期望之間的關係,則稱估計量為參數θ關於統計量T1,T2,...,...
在統計學中,估計量的偏差(或偏差函式)是此估計量的期望值與估計參數的真值之差。偏差為零的估計量或決策規則稱為無偏的。否則該估計量是有偏的。在統計中,“...
表示估計量的期望值等於真值,稱為無偏估計。如果對同一參量θ用不同估計方法得出不同的無偏估計1,2,…,其中之一κ的方差是所有估計量方差中最小的,並達到...
先驗估計是近代研究偏微分方程的一種基本方法和技巧。對偏微分方程定解問題,在解存在的假設下,通過方程係數、自由項及定解條件估計解在某個巴拿赫空間(一般是索伯...
它的均值,因而是無偏的估計。顯然,設m為有限值,當N→∞,則從式(2)可以得到漸近無偏估計。計算m個滯後數時的自相關估計約需Nm次實數乘加運算。 間接算法 ...
樣本方差也可以套用於從該分布的樣本的連續分布的方差的估計。 [2-3] 樣本方差樣本方差的無偏性 編輯 我們從一個樣本取n個值y1,...,yn,其中n <N,並根據...
