基本介紹
- 中文名:最小方差無偏估計
- 外文名:minimum-variance unbiased estimator
- 縮寫:MVUE
- 特點:擁有最小方差的無偏估計
- 領域:統計學
原理介紹







若參數函式


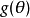


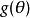
評估器選擇
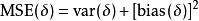
例子
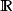










其它例子











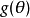


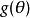
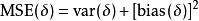
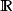











最小方差無偏估計量(minimum varianceunbiased estimator) 未知參數0的一切無偏估計中方差最小的估計量。例如,對於正態總體N(μ,o2),其簡單隨機樣本的均值x-藝x...
統計學上, 最小方差無偏估計(minimum-variance unbiased estimator,簡寫為MVUE)是一個對於所有無偏估計中,擁有最小方差的無偏估計。若無論真實參數值θ是多少,最...
若g(θ)的無偏估計量T0(X1,X2,...,Xn)對g(θ)的任意無偏估計量T(X1,X2,...,Xn)都有Var[T0]≤Var[T],則稱T0為g(θ)的一致最小方差無偏估計...
當估計值的數學期望等於參數真值時,參數估計就是無偏估計。當估計值是數據的線性函式時,參數估計就是線性估計。當估計值的均方差最小時,參數估計為一致最小均方...
在給定經典線性回歸模型的假定下,最小二乘估計量,在無偏線性估計量一類中,有最小方差,即它們滿足最優線性無偏性。...
點估計時,要求樣本統計量是無偏統計量,即要求在無數次重複抽樣時,這種樣本統計量產生的分布的平均數等於被估計的參數。還要求這個樣本分布的方差比其他無偏估計量...
的最小二乘估計482.3tr(CΣ*)是tr(CΣ)的一致最小方差不變二次無偏估計的充要條件――準正態情形522.4tr(CΣ*)是tr(CΣ)的一致最小方差不變二次無...
統計平均值在大多數情況下都是該統計量的一直最小方差無偏估計(3)阿侖方差是美國人阿侖於1966年提出的,作為頻率穩定度的表征量。阿侖方差強調取樣時間,對頻率...
相合估計(或一致估計)是在大樣本下評價估計量的標準,在樣本量不是很多時,人們更加傾向於基於小樣本的評價標準,此時,對無偏估計使用方差,對有偏估計使用均方誤差...
後者主要用於構造總體分布的數字特徵的一致最小方差無偏估計(見點估計)及基於這種估計的假設檢驗。蘇聯數學家Α.Η.柯爾莫哥洛夫和Β.И.斯米爾諾夫在20世紀30...
高斯—馬爾可夫定理(Gauss–Markov theory)是指在給定經典線性回歸的假定下,最小二乘估計量是具有最小方差的線性無偏估計量的這一定理。高斯--馬爾可夫定理的意義...
,αs的最小二乘估計,與其線性最小方差無偏估計一樣,具有相合性和漸近常態分配性質。最小二乘估計姙j(1≤j≤s)不涉及ω(t)的統計相關結構,是由數據x(1)...
式中每個平方項的權數相同,是普通最小二乘回歸參數估計方法。在誤差項等方差、不相關的條件下,普通最小二乘估計是回歸參數的最小方差的線性無偏估計。 圖集 ols...
例如,對於具有未知最大值和最小值的連續均勻分布,半極差是均值的最小方差無偏估計量,即平均值的無偏和充分估計,實際上是最小方差無偏估計:使用樣本均值僅基於該...
。從霍夫丁開始,這種統計量的大樣本性質得到了深入的研究,主要套用於構造非參數性的量的一致最小方差無偏估計(見點估計),並在這種估計的基礎上檢驗非參數性總體...
高斯馬爾科夫定理是指在給定經典線性回歸模型的假定下,最小二乘估計量,在無偏線性估計一類中,有最小方差,就是說,它們是BLUE(best linear unbiased estimator)。...
