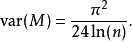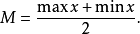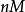基本介紹
- 中文名:半極差
- 外文名:Mid-range
- 學科:統計學
- 套用:統計分析
簡介,屬性,穩健性,效率,小樣本,採樣屬性,偏差,
簡介
屬性
穩健性
半極差對異常值非常敏感,並忽略除兩個數據點外的所有數據。因此,它是一個非常不穩健的統計數據,其故障點為0,這意味著單個觀察可以任意改變它。此外,它受異常值的影響很大:增加樣本最大值或減少樣本最小值 將改變半極差
將改變半極差 ,同時僅改變也具有分解點0的樣本均值
,同時僅改變也具有分解點0的樣本均值 。因此在實際統計中幾乎沒有用處,除非已經處理了異常值。
。因此在實際統計中幾乎沒有用處,除非已經處理了異常值。



這些調整後的半極差作為描述性統計或中心位置或偏斜的L估計值而受到關注。
效率
儘管存在缺點,但在某些情況下它是有用的:對給定一個足夠的低闊峰分布的小樣本,半極差是μ的一個高效估計量。但它對於中間分布(例如法線)是低效的。
小樣本
對於小的樣品量(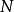 從4至20)從足夠低闊峰分布中抽取(負過量峰度,其定義為
從4至20)從足夠低闊峰分布中抽取(負過量峰度,其定義為 ,半極差是一種有效的估計平均
,半極差是一種有效的估計平均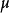 。下表總結了比較不同峰度分布均值的三個估計量的經驗數據;所述改性平均是截短的平均值,其中,所述最大值和最小值被消除。
。下表總結了比較不同峰度分布均值的三個估計量的經驗數據;所述改性平均是截短的平均值,其中,所述最大值和最小值被消除。

採樣屬性