反覆殘差法

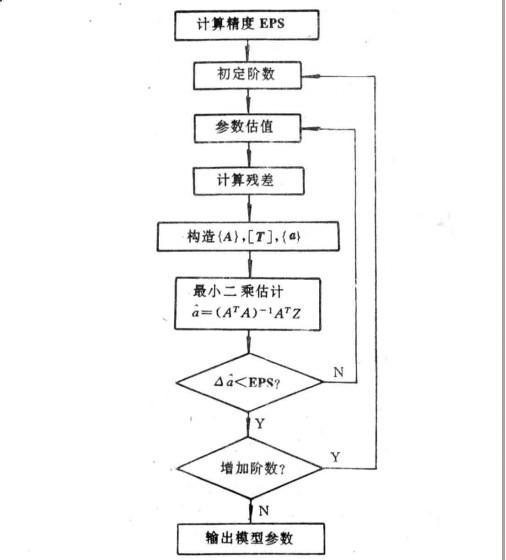
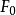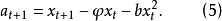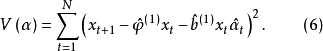反覆殘差法將模型線性化的一種疊代算法，由Subba Rao在處理雙線性模型時提出。 Subba Rao提出了反覆殘差法估算模型參數，該法是在假定模型階數、模型參數初值和計算精度條件下，計算模型殘差平方和，在最小二乘意義下使其極小化，估計新的參數值，再求殘差平方和。如此反覆疊代，直到滿足要求的精度，這時的參數值即為所求。模型定階採用AIC。反覆殘差法有計算量大，操作不便的缺點。

基本介紹

• 中文名：反覆殘差法
• 所屬學科：數學
• 基本介紹：將模型線性化的一種疊代算法
• 提出者：Subba Rao

基本介紹

雙線性差分方程 對零均值時序 擬合的雙線性模型為:

記該模型為BM(n，m，p，q)，其中，殘差 為方差是 的白噪聲，當 是非零均值時，上式中還應有一常數項 。

式(1)較ARMA (n， m)模型多一個雙線性項，即當 固定時，變成關於 的線性模型，當 固定時，變成了關於 的線性模型，因而稱之為雙線性模型。可以把雙線性模型視為ARMA模型的推廣。但是，由於它是非線性模型，模型的定階準則，穩定性與可逆性等比ARMA模型的複雜得多，計算也困難得多。對某些較簡單的雙線性模型，建模時可沿用線性系統的定階準則，如F檢驗，AIC準則等。

在階數已確定的情況下，對於雙線性模型的參數估計問題，原則上與線性模型的處理方法相同，現敘述如下，在式(1)中，當N足夠大時，有似然函式，

式中， 為參數的集合，

於是， 的極大似然估計為使殘差平方和 達最小，即 對 中每個元素取極小化而得到，因此，關於ARMA模型的建模方法如Levinson算法一般均適用於雙線性建模。Subba Rao提出的“反覆殘差法”對較為簡單的雙線性建模頗為方便有效，其思路可由圖1說明。圖中Z是由{x_t}中的元素構成的列向量，A是 與 所構成的己知的常數矩陣， 是式(2)所示的模型參數構成的列向量，反覆殘差法是在模型階數已知的條件下建模。

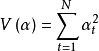
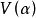
實例分析

下面是一個簡單的雙線性模型的建模過程。

設要建立的雙線性模型為:

即

式中，B為後移運算元，當b較小時，近似地有

即

忽略 項，則有

於是可套用最小二乘法估計參數φ、 b，如不忽略 項，則可套用非線性最小二乘法估計參數。

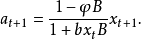
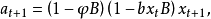
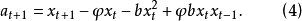
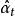設參數的初始估值為 ， 則由式(5)可得其殘差的初值 ，根據式(3) 求殘差平方和 。

在最小二乘意義下使其極小化，估計新的參數值 ，再將新參數代入式( 3)求殘差，

求出新的殘差後，再代入式(6)，估計新的參數 ，如此反覆疊代，直到滿足精度為止。

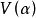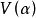
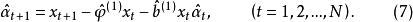
仿真建模實例

設雙線性差分方程為:

圖1所示為該雙線性系統的時間序列，系統的輸入 是方差 的零均值的白噪聲，圖2所示為雙線性時序的機率密度分布圖，其中虛線為實際分布，實線為常態分配，可見該序列已不是常態分配；圖中示出了序列的均值、方差、偏態值與峰態值，從中也可看出其非線性的特性。表1列出了雙線性建模的結果。其中，F₀為模型中含有的常數項，以便於擬合均值不為零的時序，將表中結果與式(8) 比較可知，兩者符合情況較好，表明反覆殘差法建模是有效的。

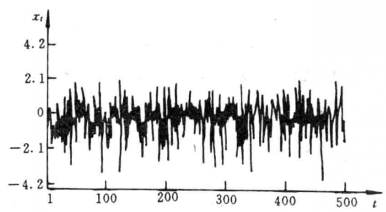圖1 雙線性時間序列

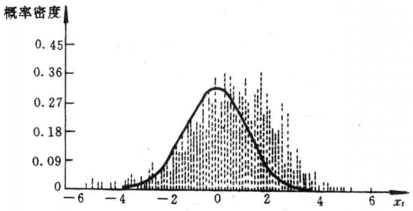圖2 雙線性序列的機率密度分布

均值：-0.317177 偏態：-0.347777 方差：1.543746 峰態：1. 005134

表1 雙線性建模結果

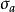			AIC值	EPS	F0
0.409	0.401	0.856	-0.3	0.001	5. 056X 10^-3