概連續映射(almost continuous mapping)亦稱幾乎連續映射，是一類廣義連續映射。
基本介紹
- 中文名：概連續映射
{設X,Y為拓撲空間，f:X-}Y.若對於任意xEX及f (x)的任意鄰域V,cl f-' (V)是x的鄰域，{則稱f為概連續映射.映射f:X-}Y是概連續的若且唯若對於Y的任意開集v,
概連續映射
概連續性沒有遺傳性，即空間x上定義的概連續映射在x的子空間上未必是概連續的.弱連續映射未必是概連續的.開的弱連續映射是概連續的.次弱連續的概連續映射是弱連續的.
概連續映射
相關詞條
- 概連續映射
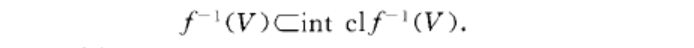
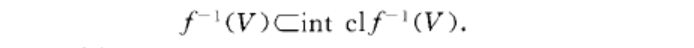
概連續映射(almost continuous mapping)亦稱幾乎連續映射，是一類廣義連續映射。{設X,Y為拓撲空間，f:X-}Y.若對於任意xEX及f (x)的任意鄰域V,cl f-' (V)是x的鄰域，{則稱f...
- 連續映射
連續映射的ε-δ語言描述 連續映射用ε-δ語言描述必須分成在一點連續與在定義域上連續兩個階段來定義，且適用於兩個度量空間之間的映射：定義1 設X和Y是兩個度量空間，映射f：X→Y;x0∈X，y0=f(x0).若對任一以y0為中心、ε>0為半徑的開球 (ε)，存在以x0為中心、δ>0為半徑的開球 (δ)，使f(...
- 概連續集值映射
概連續集值映射 概連續集值映射(almost continuous set-valuedmapping)亦稱幾乎連續集值映射一類特殊的集值映射.設F為拓撲空間X到拓撲空間Y的集值映射，xEX.若對於Y中滿足條件F'(二)CU的任意開集U,F+(U)是二的鄰域，則稱F在點二是概上半連續的.若對於Y中滿足F ...
- 全連續映射
全連續映射是映有界集為相對緊集的連續映射，緊連續映射必為全連續映射。簡介 全連續映射是映有界集為相對緊集的連續映射。設Ω⊂X，f:Ω→Y是連續映射。若對於Ω中的任何有界子集S，是Y中的緊集，則稱f為全連續映射。性質 緊連續映射必為全連續映射。當Ω為有界集時，Ω上的全連續映射與緊連續映射是等價的...
- θ連續映射
θ連續映射 θ連續映射(θ-continuous mapping)一類廣義連續映射。設X,Y為拓撲空間，映射.f:X-Y.若對於任意xEX及f(x)的任意鄰域V，存在二的鄰域U，使得 則稱f為B連續映射.連續映射是近乎連續的.近乎連續映射是B連續的.B連續映射是弱連續的.反之一般不成立.若像空間Y為正則空間，則四者一致.
- 連通映射
連通映射 連通映射是一類映射.設X,Y為拓撲空間，由映射f : X-＞Y可確定映射。連通映射，一類映射.設X,Y為拓撲空間，由映射f : X-＞Y可確定映射 若對於X的任意連通子集A,g(A)是XXY的連通子集，則稱f為連通映射.連通映射是使連通集的圖像是連通集的映射.
- 圖像連續映射
圖像連續映射 圖像連續映射(graphically continuous map-ping)一類廣義連續映射。圖像連續映射，一類廣義連續映射.設X,Y為拓撲空間，.fX -＞Y.若對於包含f的圖像G(f)的任意開集W,存在連續映射g:X-Y，使得G(g)CW，則稱f為圖像連續映射.圖像連續映射是閉遺傳的.
- 一致連續映射
一致連續映射(uniformly continuous mapping)是一致空間上的一類重要映射。映射是數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係，G的定義域D(G)為X，且對任何x∈X都有惟一的y∈Y滿足G(x，y)，則稱G為從X到Y的映射。一致空間的概念是韋伊(Weil，A.)於1938年引入的。布爾巴基(Bourbaki，N.)...
- 半連續映射
在一般拓撲學中，半連續映射是一類廣義連續映射。在泛函分析中，半連續映射即有限1-弱連續映射，是限制在定義域中過每點的一維線性流形上是連續的映射。簡介 一般拓撲學 半連續映射是一類廣義連續映射。設X,Y為拓撲空間，映射f:X→Y。若對於Y的任意開集V，f(V)是X的半開集，則稱f為半連續映射。泛函分析 半...
- 概開映射
almost open mapping)一類廣義開映射。概開映射(almost open mapping)一類廣義開映射.設X,Y為拓撲空間，f:X->Y.若對於X的任意開集U,則稱f是概開映射.f是概開映射若且唯若對於Y的任意開集v,f-1(ctv}cclf-}(v}.開映射是概開的，反之，概開映射未必是開的.概開且弱連續的映射是近乎連續的且概連續的.
- 邊緣連續映射
邊緣連續映射 邊緣連續映射是數學術語。邊緣連續映射，一類映射.設X,Y為拓撲空間，映射f:X-Y.若對於任意xEX，二的任意開鄰域(U與fx')的任意開鄰域V，存在包含於L'的二的開鄰域G，使得 其中b(G)表示G的邊界，則稱了為邊緣連續映射.
- 擬連續映射
擬連續映射 擬連續映射(quasi continuous mapping)一類廣義連續映射.設X,Y為拓撲空間，xEX,f:X-Y.若對於f(x)的任意開鄰域V和二的任意開鄰域U，存在開集G必，使得GCU與f(G)CV，則稱f在點二是擬連續的.若f在X的任意點都是擬連續的，則稱f為擬連續映射.
- 緊連續映射
緊連續映射（compact continuous mapping）是像集為相對緊集的連續映射，簡稱緊映射。簡介 緊連續映射是像集為相對緊集的連續映射。設X和Y是拓撲空間，Ω⊂X，f:Ω→Y是連續映射。若 是緊集，則稱f為緊連續映射，或簡稱緊映射。連續映射 (continuous mapping)連續映射拓撲空間之間的一類重要映射。設(X,T)與(Y,...
- ε連續集值映射
ε上半連續集值映射 (ε-upper semicontinuous setvalued mapping )ε上半連續集值映射對度量空間中的集值映射提出的一種特殊的上半連續性概念。設X是拓撲空間，(Y,d)為度量空間。F:X→2是集值映射，x₀∈X。若對於任給的ε>0，存在x₀的鄰域U，使得 其中 ，則稱F在x₀為ε上半連續。若F在X中...
- 光滑映射在一點穩定性
光滑映射在一點穩定性(stability of asmooth mapping at a point)是指光滑映射在一點局部經小擾動後本質不變的特性。光滑映射是一類連續映射，是微分拓撲學的基本概念和主要研究對象。它是微分流形之間在每點附近的局部表示。概念 光滑映射在一點穩定性(stability of asmooth mapping at a point)是指光滑映射在一點...
- 映射空間
為一個拓撲空間，則映射空間 (點式收斂拓撲)為 空間 Y為平庸拓撲空間，或者X為至多可數集並且Y為 空間。定理2 設X為任一集合，Y為一個拓撲空間，則映射空間 (點式收斂拓撲)為 ( 正則，完全正則，連通，路連通，緊緻)空間 Y為 ( ，正則，完全正則，連通，道路連通，緊緻)空間。對於連續映射，我...
- 完全映射
完全映射(perfect mapping)亦稱完備映射。一類重要的映射。設X，Y為拓撲空間，映射f：X→Y。若對於任意y∈Y，f(y)是X的緊集，則稱f為緊映射。若f是緊的、閉的且連續的映射，則稱f為完全映射。緊空間到豪斯多夫空間的連續映射是完全映射。在完全映射下緊集的原像是緊集。兩個完全映射的複合映射是完全映射。完...
- 同倫映射
同倫映射(homotopic maps)是拓撲學中的重要概念。應該指出，映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合C(X，Y)上的一個等價關係，它將這些映射分成一些等價類，稱每個等價類為一個同倫類。研究映射的同倫分類問題是同倫論的基本內容之一。概念 同倫映射(homotopic maps)是拓撲學的重要概念。直觀地說，...
- 近乎連續映射
近乎連續映射 近乎連續映射是一個數學術語。近乎連續映射(nearly continuous mapping)一類廣義連續映射.設X,Y為拓撲空間·, f: X->v.若對於任意xEX及f(x)的任意鄰域v，存在二的鄰域U，使得 則稱f是近乎連續映射.弱連續映射、概連續映射、近乎連續映射是互相獨立的.開的近乎連續映射是概詐純的.
- 映射提升定理
映射提升定理(map lifting theorem)是關於覆疊空間的一條定理。設(X'，p)是X的覆疊空間，對於連續映射f：Y→X，若存在連續映射f'：Y→X'，滿足條件p°f'=f，則稱f'為f的提升。映射提升定理：若Y是連通且局部道路連通空間，r∈Y，(X'，p)是X的覆疊空間，a∈X，b∈p(a)，則連續映射：存在提升：的...
- 鄰近連續映射
鄰近連續映射(proximally continuous mapp-ing)鄰近空間上的一類重要映射.設(X,})與(Y,澎)是兩個鄰近空間，映射f:X}Y.若對於任意A,BCX，由AFB可推出f(A)}' f(B)，則稱f.關於占與夕是鄰近連續的，簡稱f是鄰近連續映射.鄰近連續映射關於由鄰近誘導的拓撲是連續的.若f是單滿映射，且f和f-,都是鄰近連續...
- 單純映射
單純映射(simplicial map)是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射，任何連續映射在某種意義下可用它逼近，可簡記為f：K→L(省去多面體|K|，|L|的記號)。單純映射是連續映射；單純映射由限制在頂點集上的映射f⁰=f|K⁰： K⁰→L⁰完全決定。反之...
- 開映射
證明：設 f: X→Y為平庸空間X到離散空間Y的映射， 因為 包含於Y， 而Y為離散空間， 所以 和 為 Y 中的開集，即f是一個開映射。（3）設 X 和 Y 是兩個拓撲空間，映射 為同胚，則映射 為一個開映射。證明：設U是X的任意開集，由於映射 為同胚， 則 也是同胚， 因而 是連續映射。對X的...
- 映射芽
映射芽(germ of mapping)是奇點理論與突變理論的主要研究對象之一。確定在一點的鄰域上的連續映射的等價類，精確地說，設X，Y是拓撲空間，p∈X，考慮由在點p附近定義的全體連續映射g所構成的集合A，A={g|g：U→Y，U是點p的開鄰域，g是連續映射}，在這個集合里引進等價關係如下：設g：U→Y，f：V→Y是A...
