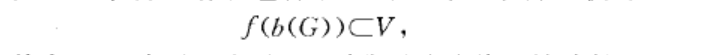
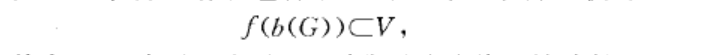

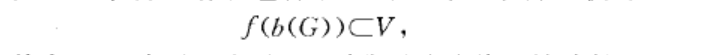
邊緣連續映射是數學術語。邊緣連續映射(peripherally continuous map-ping)一類映射.設X,Y為拓撲空間,映射f:X-Y.若對於任意xEX,二的任意開鄰域(U與fx')的任意開鄰域V,存在包含...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,因而它應將閉鏈與邊緣鏈分別映成閉鏈與邊緣鏈。概念 單純鏈映射(...
8.1 閉鏈與邊緣 8.2 同調群 8.3 例子 8.4 單純映射 8.5 輻式重分 8.6 不變性 第9章 映射度與Lefschetz數 9.1 球面的連續映射 9.2 Euler?Poincaré公式 9.3 Borsuk?Ulam定理 9.4 Lefschetz不動點定理 9.5 維數 第...
同調論關係於邊緣的概念,例如三維空間中球的邊緣是它的二維球面,而二維球面的邊緣是零。邊緣運算元的這種規範性質亦可在純代數的構架內再現; 這就是同調代數的基本要素。同倫論關係於圖形和映射在連續形變下所保持的性質。同倫 設f、g是...
所謂拓撲學,簡要地說,就是研究空間圖形在連續變換下不變的性質。換言之,在原來圖形的點與變換了的圖形的點之間存在一個一一對應,並且鄰近的點變成鄰近的點,這一性質叫做連續性,該變換叫做拓撲變換。拓撲性質有那些呢?首先我們介紹...
設f、g是拓撲空間X到Y的兩個連續映射,若存在連續映射H:X×I→Y使得:H(x,0)=f(x)H(x,1)=gx∈X 則稱f與g同倫,記為f≃g:X→Y或f≃g,映射H稱為f與g之間的一個同倫。f與g的同倫H也可理解為單參數映射族{...
8.1 閉鏈與邊緣 8.2 同調群 8.3 例子 8.4 單純映射 8.5 輻式重分 8.6 不變性 第9章 映射度與Lefschetz數 9.1 球面的連續映射 9.2 Euler Poincaré公式 9.3 Borsuk Ulam定理 9.4 Lefschetz不動點定理 9.5...
與同調群的定義相似,可以定義以G為係數的上閉鏈群Zn(K;G),上邊緣鏈群Bn(K;G),上同調群Hn(K;G)。當G為整數加群Z時,省去符號Z,簡單記為 Cn(K),Zn(K),Bn(K),Hn(K),等等。對於連續映射F:│K│→│L│,利用...
是一個連續映射(假設 )。則我們可以構造胞腔復形 這裡 是2n-維圓盤通過 貼上一個 。 胞腔鏈群 在度數n只是由n-胞腔自由生成,故它們在度數 0、n 與 2n是 ,其餘都是零。胞腔(上)同調是該鏈復形的(上)同...
分別稱為q維上閉鏈群與上邊緣鏈群。商群:H(K)=Z(K)/B(K) (q∈Z)稱為復形K的q維上同調群,這些群中元素分別稱為上閉鏈、上邊緣鏈與上同調類。相應原來的同調群可稱為下同調群。設f:K→L是單純映射,f={f:C(K)...
它的前身是點集拓撲學。 一般拓撲學的歷史約六十年,由於它適應了科學的發展,其生命力是相當旺盛的。由於一般拓撲學的建立,一些邊緣學科也相繼產生,於是,拓撲學及與拓撲學密切相關的學科在純粹數學中的地位愈來愈重。
