同倫運算元(homotopy operator)是具有同倫性質的線性變換。
兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。
基本介紹
- 中文名:同倫運算元
- 外文名:homotopy operator
- 領域:數學
- 性質:線性變換
- 特點:同倫
- 對象:微分流形
概念

同倫
線性變換

同倫運算元(homotopy operator)是具有同倫性質的線性變換。
兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。

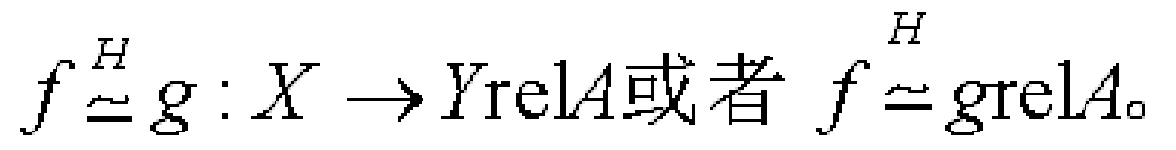

同倫運算元(homotopy operator)是具有同倫性質的線性變換。兩個拓撲空間X和Y同倫等價的充要條件是:存在空間Z,使得X與Y分別同胚於Z的兩個強形變收縮核。概念同倫運算元(homotopy operator)是具...
《同倫反演算法及其在地球物理領域中的套用》是依託哈爾濱工業大學,由劉家琦擔任項目負責人的面上項目。項目摘要 以地震勘探、石油測井中的實際問題為背景,在國內外首次將求解非線性運算元方程的大範圍收斂方法——同倫法引入地球物理反問題...
為了得到整體性的同胚,僅用微分學是不夠的,藉助於緊性概念以及拓撲學中的同倫概念可以得到整體的反函式定理:為了使連續映射ƒ是一個同胚,必須且僅須它是局部同胚,並有ƒ是固有的。所謂運算元ƒ是固有的,指緊集的原像是緊集。Y...
並且,Chas和Sullivan還證明,這個同倫運算元形成一個準李代數(pre-Lie algebra),因而它的交換子形成一個李代數;這個李代數和上面的交換結合代數滿足Gerstenhaber代數所必須的兼容條件,從而我們在自由環路空間的同調群上得到一個Gersten...
建立作用於微分形式上的重要運算元及其複合運算元的積分估計式,如格林運算元、同倫運算元等。進一步將得到的相關結果推廣到重要的區域,如John域及黎曼流形上。給出A-調和張量與相關運算元的有界性、緊性的條件,進一步深入研究A-調和方程理論。結合...
鏈復形(chain complex)是一種抽象的復形。復形常指上復形。上復形亦稱上鏈。一種特殊的模同態序列。類似地可定義和討論與鏈復形有關的鏈映射、鏈同倫以及鏈復形的同調序列等同調理論。從單純同調群和奇異同調群的理論可看出這些...
在第一方面,對於刻畫非線性界面波的耦合偏微分方程組,同倫分析方法得到進一步的發展和改進,通過引進耦合線性運算元和矩陣逆運算,克服了解耦線性運算元求解導致級數解發散的缺點,對於同倫分析方法的完善和套用具有重要影響,也就是在強非線性解...
coboundary operator 邊緣運算元英語 ; 上邊緣運運算元 ; 翻譯 ; [數] 上邊緣運算元 coboundary homomorphism[數] 上邊緣同態 homotopy coboundary operation[數] 同倫上邊緣運算 ; 同倫余緣運算 y coboundary operation 同倫上邊緣運算 Sweed...
性質2——同倫 設f、g是拓撲空間X到Y的兩個連續映射,若存在連續映射H:X×I→Y使得:H(x,0)=f(x)H(x,1)=gx∈X 則稱f與g同倫,記為f≃g:X→Y或f≃g,映射H稱為f與g之間的一個同倫。f與g的同倫H也可理解...
自然地,非自伴運算元代數中的指標理論需要得到深入的研究。在本課題中,我們將研究典型的非自伴運算元代數- - 套代數的指標理論。我們擬從指標是否是套代數中Fredholm運算元的完全同倫不變數這一核心問題入手,研究套代數中的指標理論的相關...
50年代以來,即問兩個映射,以R.H.賓為代表的美國學派的工作加深了對流形的認識,是問兩個給定的映射是否同倫,在四維龐加萊猜想的證明中發揮了作用。從皮亞諾曲線引起的維數及連續統的研究,習慣上也看成一般拓撲學的分支。代數拓撲...
第五章一般非線性運算元的全局性理論 5.1線性化 5.2有限維逼近 5.3同倫,映射底及其推廣 5.4同倫和非線性運算元的映射性質 5.5對非線性邊值問題的套用 第六章梯度映射的臨界點理論 6.1極小化問題 6.2來自幾何學與物理學的具體極...
將A射到其極分解里的酉部分U是一個從一般線性群GL(n,C) 射到酉群U(n) 的映射。這是一個同倫等價,因為所有正定矩陣構成的空間是一個可縮空間。實際上,U(n) 是 GL(n,C) 的極大緊子群。有界運算元 從復希爾伯特空間到復...
實際上,如果│K│,│L│倫型相同,其同倫等價也誘導它們的上同調群、同調群的同構。利用同調群可以解決不少幾何問題。例如,布勞威爾不動點定理(見不動點理論),可以找到歐拉示性數與貝蒂數之間的關係式:其中αi為復形K的i維...
