θ連續映射(θ-continuous mapping)一類廣義連續映射。
基本介紹
- 中文名：θ連續映射
- 外文名：θ-continuous mapping
設X,Y為拓撲空間，映射.f:X-Y.若對於任意xEX及f(x)的任意鄰域V，存在二的鄰域U，使得
θ連續映射
則稱f為B連續映射.連續映射是近乎連續的.近乎連續映射是B連續的.B連續映射是弱連續的.反之一般不成立.若像空間Y為正則空間，則四者一致.
θ連續映射
相關詞條
- θ連續映射
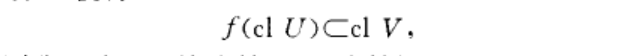
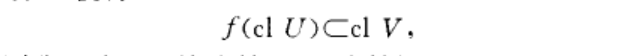
θ連續映射(θ-continuous mapping)一類廣義連續映射。設X,Y為拓撲空間，映射.f:X-Y.若對於任意xEX及f(x)的任意鄰域V，存在二的鄰域U，使得則稱f為B連續映射.連續映射是近乎連續的.近乎連續...
- 連續映射
連續映射的ε-δ語言描述 連續映射用ε-δ語言描述必須分成在一點連續與在定義域上連續兩個階段來定義，且適用於兩個度量空間之間的映射：定義1 設X和Y是兩個度量空間，映射f：X→Y;x0∈X，y0=f(x0).若對任一以y0為中心、ε...
- 全連續映射
全連續映射是映有界集為相對緊集的連續映射，緊連續映射必為全連續映射。簡介 全連續映射是映有界集為相對緊集的連續映射。設Ω⊂X，f:Ω→Y是連續映射。若對於Ω中的任何有界子集S，是Y中的緊集，則稱f為全連續映射。性質 緊連續...
- 可微映射度
可微映射度(degree of differential map)是重要的同倫不變數。同倫論是拓撲學的重要概念。應該指出，映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合上的一個 等價關係，它將這些映射分成一些等價類，稱每個等價類為一個同倫類。
- 連續統和拓樸動力系統中的若干問題
證明了SUSLIN遺傳θ連續統上自同胚的熵為零，遺傳可分可鏈體上誘導自同胚的熵為零，逐段單調熵為零的區間自映射的逆極限空間為SUSLIN的。引入不可分概念並以此為出發點把樹上連續自映射動力學的研究的諸多方面作了統一處理。在樹上...
- 一致連續映射
一致連續映射(uniformly continuous mapping)是一致空間上的一類重要映射。映射是數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係，G的定義域D(G)為X，且對任何x∈X都有惟一的y∈Y滿足G(x，y)，則稱G為從X到Y的...
- 閉映射
（4）定義從[0,2π)到單位圓（視為R中的圓，原點為圓心）的函式：在[0,2π)中的θ所對應的值，是單位圓上與x軸成角度θ的點。這個函式是雙射連續的，所以其從單位圓到[0,2π)的逆函式是既開且閉的。這個逆函式將緊緻的...
- ε連續集值映射
ε上半連續集值映射 (ε-upper semicontinuous setvalued mapping )ε上半連續集值映射對度量空間中的集值映射提出的一種特殊的上半連續性概念。設X是拓撲空間，(Y,d)為度量空間。F:X→2是集值映射，x₀∈X。若對於任給的ε...
- 擬一致連續映射
擬一致連續映射是數學術語。擬一致連續映射(quasiuniformly continuousmapping)擬一致空間上的一類重要映射.設(X,') , (Y,`y')為兩個擬一致空間，f :XY.若對於任意VE`y、存在UE'u，使得當(二，y＞ E U時有(f(二)，fCy)) ...
- 微連續映射
微連續映射是一個數學術語。微連續映射(faintly continuous mapping)一類廣義連續映射.設X,Y為拓撲空間，映射.f : X-Y.若Y的任意B開集的原像是X的開集，則稱f為微連續映射.設VCY.若V包含它的每點的一個閉鄰域，則稱V為Y的B...
- 概連續映射
概連續映射(almost continuous mapping)亦稱幾乎連續映射，是一類廣義連續映射。設X,Y為拓撲空間，f:X-}Y.若對於任意xEX及f (x)的任意鄰域V,cl f-' (V)是x的鄰域，則稱f為概連續映射.映射f:X-}Y是概連續的若且唯若對於Y...
- 上半連續映射
上半連續映射 上半連續映射（upper semi-continuous mapping）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
- C連續映射
C連續映射(C-continuous mapping)一類廣義連續映射.設X,Y為拓撲空間，映射f:XY.若對於任意二EX及f(二)的任意具有緊補的開鄰域V，存在x的開鄰域U，使得f (U＞CV，則稱f是C連續映射.f是C連續映射若且唯若對於Y的任意閉緊子集C...
- 弱連續映射
弱連續映射是一類廣義連續映射。設X,Y為拓撲空間，f:X→Y，x∈X。若f在x的任意點都是弱連續的，則稱f是X上的弱連續映射。簡介 弱連續映射是一類廣義連續映射。設X,Y為拓撲空間，f:X→Y，x∈X。若對於f(x)的任意鄰域V，...
- 概連續集值映射
概連續集值映射(almost continuous set-valuedmapping)亦稱幾乎連續集值映射一類特殊的集值映射.設F為拓撲空間X到拓撲空間Y的集值映射，xEX.若對於Y中滿足條件F'(二)CU的任意開集U,F+(U)是二的鄰域，則稱F在點二是概上半連續的....
- 龐加萊映射
龐加萊映射 龐加萊映射是由相空間中軌線運動定義的一種映射。當軌線反覆穿越同一截面時，反映後繼點對先行點依賴關係的映射。一個連續非線性動力系統的求解是非常困難的，法國數學家龐加萊(Poincaré，(J.-)H.)給出了相圖分析法。...
- 李普希茨條件
李普希茨連續映射(Lipschitz continuousmapping)是滿足李普希茨條件的連續映射。設有映射 ，若有正常數L，使得 則稱 為李普希茨連續映射，其中正常數L稱為李普希茨常數，(1)式表達的條件稱為李普希茨條件。李普希茨連續映射必是一致...
- 非線性運算元
是某個弱連續泛函φ的導運算元時，又若 A x≠θ對任意的x≠θ,則存在с≠φ(θ)，使得流形，模平方函式‖x‖在M 0上達到極小值點。這個極小值點就是 A 的特徵元,而對應的拉格朗日乘子則是非線性特徵值的倒數。φ 還是偶泛函...
- 同調論(現代數學的一門重要基礎課)
對於連續映射F：│K│→│L│,利用單純映射去逼近，可得到同態。上同調群的構造可以由同調群完全確定。當多面體│K│為定向流形時，同調群和上同調群之間還有對偶關係（流形的龐加萊對偶定理）,即Hn(|K|;G)同構於Hq-n(│K│;G)...
- 上同調環
若f：X→Y是連續映射，則f*：H*(y)→H*(X)是環同態。倫型相同的空間的上積構造是同構的。設c∈△(X)，σ是X中任一(p+q)奇異單形，定義卡積∩為c∩σ=(c，σθₚ>σθ，對dimc>dimσ規定c∩σ=₀作線性擴張，...
- 複變函數(以複數作為自變數和因變數的函式)
)之間的一個映射。例如在w=z₂的映射下，z平面上的射線argz=θ與w平面上的射線argw=2θ對應；如果ƒ(A)∈A*，稱ƒ把A映入A*。如果ƒ(A)=A*，則稱ƒ把A映成A*，此時稱A為A*的原像。對於把A映成A*的映射ƒ...
- 拓撲動力系統
從20世紀70年代以來，由於微分動力系統研究的發展和深入，極大地推動了拓撲動力系統，特別是一維連續映射的研究，並取得了相當豐富和重要的成果。滿足條件 ① 初值條件：φ(x,0)=x；② φ(x,t)對x，t一併連續；③ 群的條件：即對...
