完全映射(perfect mapping)亦稱完備映射,一類重要的映射。設X,Y為拓撲空間,映射f:X→Y。若對於任意y∈Y,f(y)是X的緊集,則稱f為緊映射。若f是緊的、閉的且連續的映射,則稱f為完全映射。
基本介紹
- 中文名:完全映射
- 外文名:perfect mapping
- 領域:數學
- 學科:函式
- 別稱:完備映射
- 性質:一類重要的映射
概念
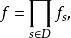
完全映射(perfect mapping)亦稱完備映射,一類重要的映射。設X,Y為拓撲空間,映射f:X→Y。若對於任意y∈Y,f(y)是X的緊集,則稱f為緊映射。若f是緊的、閉的且連續的映射,則稱f為完全映射。
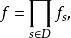
完全映射(perfect mapping)亦稱完備映射,一類重要的映射。設X,Y為拓撲空間,映射f:X→Y。若對於任意y∈Y,f(y)是X的緊集,則稱f為緊映射。若f是緊的、閉的...
在數學裡,映射是個術語,指兩個元素的集之間元素相互“對應”的關係,為名詞。映射,或者射影,在數學及相關的領域經常等同於函式。 基於此,部分映射就相當於部分...
在有限元分析中,形狀不規整的實際單元(參數單元)和形狀規整的標準單元之間可以建立坐標變換,如果坐標變換和試探函數裡的形函式、插值節點完全相同,就稱為等參數映射...
單純映射(simplicial map)是聯繫復形的多面體之間的一類重要映射。它是從復形K的多面體|K|到復形L的多面體|L|的連續映射,任何連續映射在某種意義下可用它逼近,可...
擬完全映射(quasi perfect mapping)完全映射的一種推廣.設X,Y是拓撲空間,映射f:X-}Y.若、f是閉的連續映射,並且對於任意.vEY,f-'(.v)是x的可數緊子集,則...
標準部分映射(standard part map)是有限超實數集到實數集的一個映射。設Fin(*R)是一切有限超實數集,則映射st:Fin(*R)→R,st(y)=x,若且唯若x≈y,稱為...
映射空間亦稱函式空間,拓撲學的一個基本概念。它是一類重要的拓撲空間,設X,Y是集合,F為X到Y的映射組成的族,在F上引入拓撲使之成為拓撲空間,則稱F為映射空間。...
阿廷映射(Artin mapping)是理想群(或伊代爾群)到伽羅瓦群的映射。它是類域論的基石之一。伊代爾群是一種特殊的群。即各分量為諸局部域元素的某些向量(其分量幾乎...
單純鏈映射(simplicial chain map)是由單純映射決定的鏈映射。鏈映射是聯繫復形的鏈群之間的一種系列同態。為了使復形的鏈群之間的同態能誘導出同調群之間的同態,...
碼映射(coding mapping)是符號空間Ωω到切餅集C上的一種映射。...... 基於此,部分映射就相當於部分函式,而完全映射相當於完全函式。碼映射符號空間 編輯 符號空...
帳篷映射(tent map),在數學中是指一種分段的線性映射,因其函式圖像類似帳篷而得名。...
記憶體映射檔案,是由一個檔案到一塊記憶體的映射。Win32提供了允許應用程式把檔案映射到一個進程的函式 (CreateFileMapping)。記憶體映射檔案與虛擬記憶體有些類似,通過記憶體...
偽阿諾索夫(Аносов)映射是曲面的一種同胚或微分同胚,是環面上的線性阿諾索夫微分同胚的推廣。映射是數學分析的基本概念及研究對象。映射與函式(還有變換、...
完全環(perfect ring)是一類具有同調性質的環,概念是巴斯(Bass , H.)於1960年研究模範疇的同調性質時引進的。環是對並與差運算封閉的集類,測度論中重要概念之...
k映射((k-mapping)一類特殊的映射.設X,Y是兩個拓撲空間,f:X}Y是連續映射.若對於Y的任意緊集K,f-'(K)在X中為緊集,則稱f為k映射.k映射是緊覆蓋映射....
塊映射策略是指當需要將來自記憶體的新數據塊裝入高速快取時,由塊映射策略決定它的存放位置。根據塊在高速快取內的位置,塊映射策略可分成直接映射、全相聯映射和組相...
Map,將鍵映射到值的對象。在map中可以使用匿名對象找到一個key對應的value。...... 將鍵映射到值的對象。一個映射不能包含重複的鍵;每個鍵最多只能映射到一個值...
異步映射(Asynchronous Mapping Procedure AMP),簡稱amp。對映射信號的結構無任何限制(信號有無幀結構均可),也無需與網路同步(例如PDH信號與SDH網不完全同步)。利用...
自適應共振理論映射ARTMAP(Adaptive Resonance Theory Map)是美國Boston大學的S.Grossberg和A.Carpenet在1976年提出的。ART是一種自組織神經網路結構,是無教師的學習...
定義介紹 完全可分配性(completely distributivity)可分配律的推廣.對於任意兩個集合s和W,用sw表示由W到s中的所有映射的集合.給定一個由Wxs到布爾代數B的映射,它...
《圓映射》是1998年上海科技教育出版社出版的圖書,作者是陳式剛。...... 《圓映射》是1998年上海科技教育出版社出版的圖書,作者是陳式剛。作者 陳式剛 ISBN ...
《完全掌握》是2013年清華大學出版社出版的圖書,作者是金昊。本書既適合喜愛數碼攝影的初、中級讀者作為自學參考書,又可以作為在婚紗影樓從事數碼照片處理或數碼沖印...
