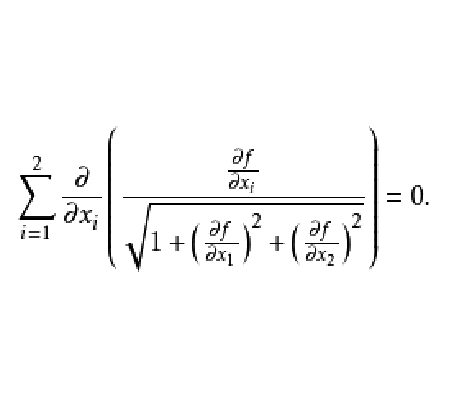極小曲面方程

極小曲面方程(minimal surface equation)是在固定邊界上的具有最小面積的曲面所滿足的方程。設Rⁿ⁺¹中的曲面方程為x_n+1=u(x)(x∈Ω)，則面積積分S=∫_Ω√(1+|Du|²₎dx的歐拉-拉格朗日方程Mu=(1/n)D_i((D_iu)/(1+|Du|²))^1/2=0即是極小曲面方程。這是一個熟知的擬線性橢圓型方程，它是更一般的指定平均曲率方程的特例。若Ω是Rⁿ中的有界C²區域，則狄利克雷問題Mu=0(在Ω內)，u=φ(在∂ Ω上)對任意φ∈C⁰(∂ Ω)有解的充分必要條件是邊界∂ Ω的平均曲率處處非負。

基本介紹

• 中文名：極小曲面方程
• 外文名：minimal surface equation
• 定義：極小曲面所滿足的微分方程
• 屬性：偏微分方程
• 相關概念：極小曲面、微分方程、平均曲率等

定義

表述1 極小曲面方程(minimal surface equation)是偏微分方程和微分幾何中的一個非常重要的方程，它是極小曲面所滿足的微分方程。設{，D為中的一區域}為中的一極小曲面，由於的平均曲率為零，所以有

此方程稱為極小曲面方程。

表述2 設中的曲面方程為，則面積積分

的歐拉-拉格朗日方程

即是極小曲面方程。這是一個熟知的擬線性橢圓型方程，它是更一般的指定平均曲率方程的特例。若Ω是中的有界區域，則狄利克雷問題(在Ω內)，(在∂ Ω上)對任意有解的充分必要條件是邊界∂ Ω的平均曲率處處非負。

相關分析

（接表述1）一般地，設為一極小浸入，局部地由所給出。換言之，相對於M中的坐標系及中的坐標系，若

及

局部地為及上的度量，則

因為M是極小的，所以對M中每一么正基，有

或等價地

其中為M的第二基本形式。將上式詳細寫出來，得

其中

分別為M及的聯絡係數，這是一個擬線性的橢圓型方程組。若是黎曼流形間的一個極小浸入，則函式必適合上述方程組。