基本介紹
- 中文名:極小化問題
- 外文名:minimization problem
- 適用範圍:數理科學
定義介紹

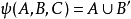
真值函式


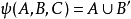

極小化問題是求出與給定電路等效的一個(或所有)最簡電路的問題。實際上極小化問題就是求與給定真值函式(一種特殊的布爾函式)的一個(或所有)最簡的等值函式。...
極小化極大(Minimax), 是一類重要的數學規劃問題,指在找出失敗的最大可能性中的最小值。極小化極大問題,雖然目標函式有時可微,但其極大值函式通常不可微,...
極小化序列(minimizing sequences)是指使泛函值的極限為泛函極小值的函式序列。設E是實Banach空間, D⊂E, f是定義在D上的實泛函。若存在{xn} ⊂D,使得:...
極小化極大決策函式(minimax decision func-tion)決策函式的一種優良準則。...... 稱極小化極大解.當問題為估計或檢驗時,也稱占’為極小化極大估計或極小化極...
從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:...
極大極小(minimax)是一類重要的不可微最佳化問題,不僅在工程設計、對策論等領域套用廣泛,而且與非線性方程組、非線性規劃、多目標規劃等數學問題之間密切相關。...
在數學中,極小曲面是指平均曲率為零的曲面。舉例來說,滿足某些約束條件的面積最小的曲面。 物理學中,由最小化面積而得到的極小曲面的實例可以是沾了肥皂液後吹...
《極大極小》是1988年四川教育出版社出版的圖書,作者是Iavn niven。...... 極大極小內容簡介 編輯 匯聚了解決極大極小問題的主要初等方法。 [1] ...
組合最最佳化的特點是:多數問題屬於所謂的NP完全問題,即對該問題基本上不存在一種算法,使得當所有的具體問題的變數和約束條件的數目兩者之和甚大時,可以在容許時間(...
在空間內以給定的閉曲線為邊緣張以肥皂膜時,表面張力使膜穩定在表面積為最小的狀態。這刺激了科學家對極小曲面的研究。因此,極小曲面問題又稱為普拉托問題。...
極小度不可解度 編輯 不可解度是遞歸論重要概念之一。指遞歸不可解的程度。在研究判定問題時,人們發現,不同的不可解的判定問題之間,不可解的程度有差別。已...
從數學意義上,最優控制過程可分為三類:拉格朗日問題、麥耶爾問題和波爾扎問題。如果已知系統的狀態方程與初始狀態,要求最優控制u(t),使得相應的積分型指標為極小,...
全局極小點一定是局部極小點,反之不然.一般來說,求全局極小點是相當困難的,因此,通常只求局部極小點(在實際套用中,有時求局部極小點已滿足了問題的要求) [...
變分問題(variational problem)是有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有:1.最速降線問題:給定不在同一鉛垂線上的兩點A和B,求出連結A...
極小子流形是一類平均曲率向量為0的子流形。極小子流形是整體微分幾何的重要課題。它與微分方程、拓撲學、幾何測度論、複變函數論等數學分支都有緊密的聯繫,並...
原問題與對偶問題是相對的,二者為同類型的規劃,構成對偶規劃的一般規則如下: [1] 若原問題是極大化問題,那么對偶問題就是極小化問題;若原問題是極小化問題,...
從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:...
從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:...
從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:廣義上,最最佳化包括數學規劃、圖和網路、組合最最佳化、庫存論、決策論、排隊論、最...
從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:廣義上,最最佳化包括數學規劃、圖和網路、組合最最佳化、庫存論、決策論、排隊論、最...
從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:...
從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:廣義上,最最佳化包括數學規劃、圖和網路、組合最最佳化、庫存論、決策論、排隊論、最...
線性二次高斯問題(linear quadratic Gaussianproblem)簡稱LQG問題,是討論高斯系統(參見“隨機控制”中系統(3),(4))在極小化二次型性能指標的問題。...
