線性二次高斯問題(linear quadratic Gaussianproblem)簡稱LQG問題,是討論高斯系統(參見“隨機控制”中系統(3),(4))在極小化二次型性能指標的問題。
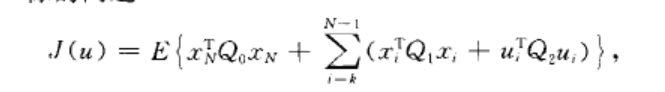
這裡Qo妻O,})O,}z}O分別是對稱半正定和對稱正定陣.當“隨機控制”條目中的(3)中無噪聲(即wk+t=0),且狀態完全量測時,相應的性能指標也不再取期望,這時稱之為線性二次問題.這時最優控制是狀態量的線性反饋uk=I k二*,I*由“隨機控制”條目中的(3)中的係數陣及}o,}t,}:所決定,它可以遞推地表達出來.對高斯系統,濾波值x*可以遞推地求得,這就是卡爾曼濾波.把濾波值x*取代相應確定性系統最優控制中的狀態二*,得到隨機控制uk_Ikxk.這就是使二次型指標達極小的最優隨機控制.所以對LQG問題成立分離原則.
