基本介紹
- 中文名:數學期望值
- 外文名:Mathematical expectation value
- 簡稱:期望
- 所屬領域:機率論;統計學
簡介
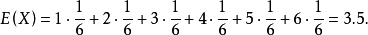
數學定義
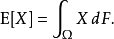
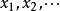
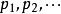
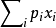
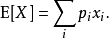
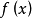
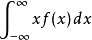
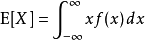
性質
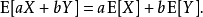
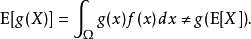
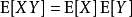
期望值的運用
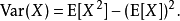

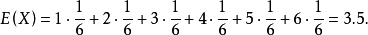
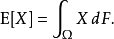
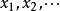
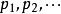
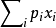
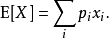
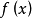
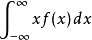
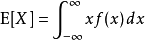
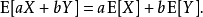
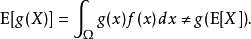
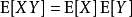
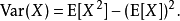
在機率論和統計學中,一個離散性隨機變數的數學期望值(或數學期望、或均值,亦簡稱期望,物理學中稱為期待值)是試驗中每次可能的結果乘以其結果機率的總和。...
在機率論和統計學中,數學期望(mean)(或均值,亦簡稱期望)是試驗中每次可能結果的機率乘以其結果的總和,是最基本的數學特徵之一。它反映隨機變數平均取值的大小。...
在機率論和統計學中,期望值(或數學期望、或均值,亦簡稱期望,物理學中稱為期待值)是指在一個離散性隨機變數試驗中每次可能結果的機率乘以其結果的總和。換句話說...
最大期望算法歷史 編輯 對EM算法的研究起源於統計學的誤差分析(error analysis)問題。1886年,美國數學家Simon Newcomb在使用高斯混合模型(Gaussian Mixture Model, ...
方差是在機率論和統計方差衡量隨機變數或一組數據時離散程度的度量。機率論中方差用來度量隨機變數和其數學期望(即均值)之間的偏離程度。統計中的方差(樣本方差)是...
平均成績相同,但X 不穩定,對平均值的偏離大。方差描述隨機變數對於數學期望的偏離程度。單個偏離是消除符號影響方差即偏離平方的均值,記為D(X):直接計算公式分離散...
均方值方差:偏差: 所以方差也稱為偏差的均方值。對於隨時間連續變化的一個變數x(也可看時 ),其數學期望可寫成:它實際上就是 的平均值 。...
隨著樣本量n的增大,不論原來的總體是否服從常態分配,樣本均值的抽樣分布都將趨於常態分配,其分布的數學期望為總體均值μ,方差為總體方差的1/n。這就是中心極限...
機率論歷史上第一個極限定理屬於伯努利,後人稱之為“大數定律”。機率論中討論隨機變數序列的算術平均值向隨機變數各數學期望的算術平均值收斂的定律。在隨機事件的...
不確定的收益可以用多種可能的取值及其對應的機率來表示,這兩者的加權平均,即數學期望值,就是資產的預期收益。 在投資理財中,預期收益的重要性,怎么強調都不為過...
均值函式是隨機過程的重要數量特徵。設{X(t),tET}是一復值隨機過程,如果對每個tET,隨機變數X(t)的數學期望m(t)=E{X(t)}存在,這時稱定義在T上的函式m (...
有:指數分布數學期望 編輯 期望值:比方說:如果你平均每個小時接到2次電話,那么你預期等待每一次電話的時間是半個小時。指數分布方差 編輯 ...
若隨機變數X服從一個數學期望為μ、方差為σ^2的常態分配,記為N(μ,σ^2)。其機率密度函式為常態分配的期望值μ決定了其位置,其標準差σ決定了分布的幅度。...
平均速率是速率分布的數學期望值:方均根速率方均根速率vrms是速率的平方的平均值的平方根:三種典型速率的關係它們具有以下的關係:1872年,玻耳茲曼創立了系統的氣體輸...
因此,上式可以成為一個分布列,此分布列是兩個幾何數列一般項的和,在這裡稱X服從兩事件下推廣的幾何分布,記為X ~ PGE(2;p) ,數學期望為: 。當P = 時,E...
