均值函式是隨機過程的重要數量特徵。設{X(t),tET}是一復值隨機過程,如果對每個tET,隨機變數X(t)的數學期望m(t)=E{X(t)}存在,這時稱定義在T上的函式m (t)為該過程的均值函式。
基本介紹
- 中文名:均值函式
- 外文名:mean function
- 適用範圍:數理科學
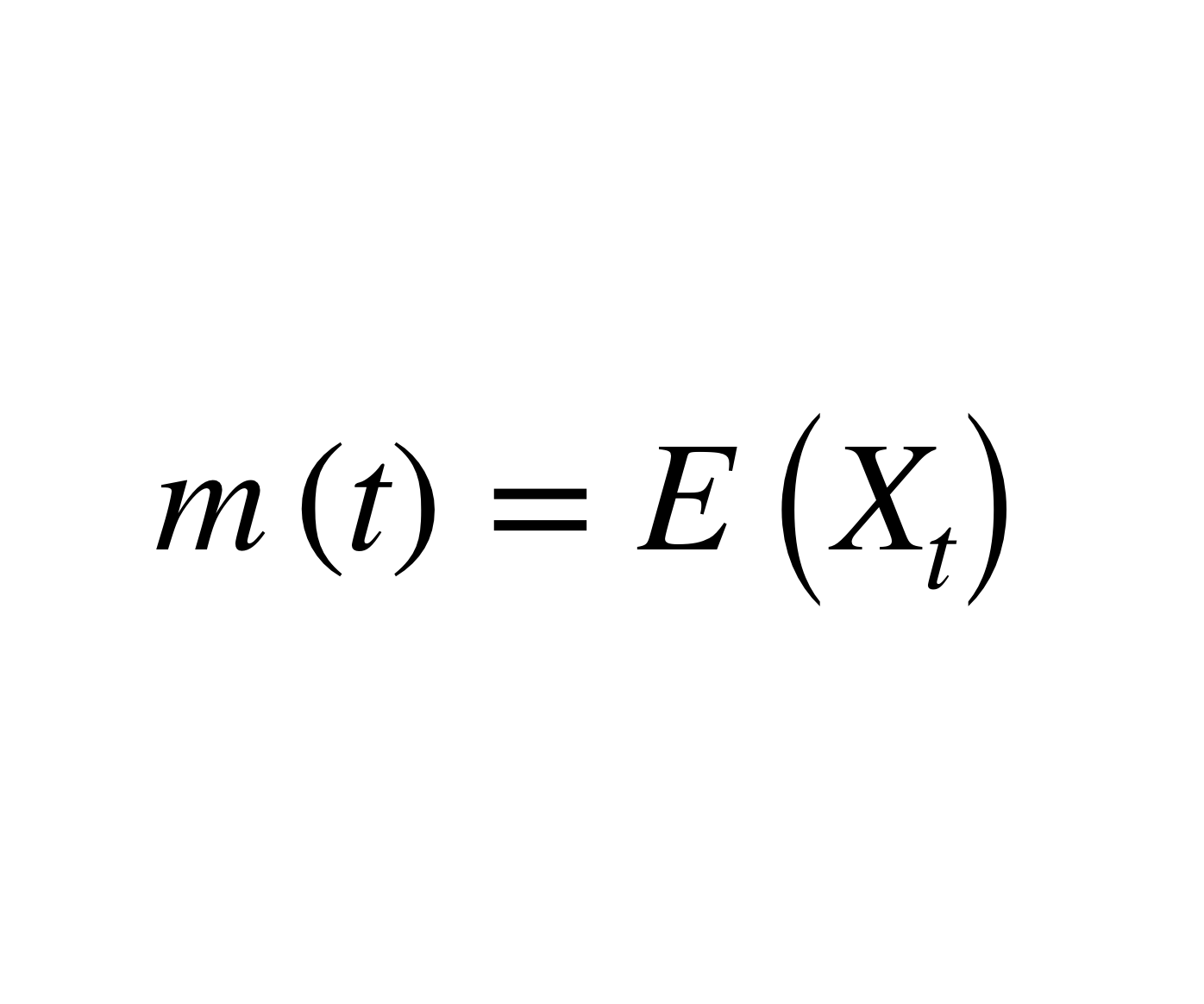
均值函式是隨機過程的重要數量特徵。設{X(t),tET}是一復值隨機過程,如果對每個tET,隨機變數X(t)的數學期望m(t)=E{X(t)}存在,這時稱定義在T上的函式m (t)為該過程的均值函式。
均值函式是隨機過程的重要數量特徵。設{X(t),tET}是一復值隨機過程,如果對每個tET,隨機變數X(t)的數學期望m(t)=E{X(t)}存在,這時稱定義在T上的函式m (...
這就是平均值定理式(1)。另外,還可以使用δ函式來證明平均值定理[1] 。平均值定理套用 編輯 平均值定理在理論研究上是很有用的。另外,它還可以用在近似計算上...
均值定理,又稱基本不等式。主要內容為在正實數範圍內,若干數的幾何平均數不超過他們的算術平均數,且當這些數全部相等時,算術平均數與幾何平均數相等。均值定理是...
均值方差模型假定,如果投資者獲得財富W時的機率為π,那么,這個機率分布的效用就可以表示為該分布的均值和方差的函式u(υ,υ2)。或者,如果更方便,效用也可以表示...
均值—方差模型是由H.M.Markowitz(哈里·馬科維茨)在1952年提出的風險度量模型。馬科維茨把風險定義為期望收益率的波動率,首次將數理統計的方法套用到投資組合選擇...
AVG SQL資料庫中求平均值函式 AVG SQL資料庫中求平均值函式avg()用於對指定的列或表達式求平均值。當使用avg()函式對指定列求平均值時,如果該列存在空(NULL)...
averageifs函式是一個求平均值函式,主要是用於返回多重條件所有單元格的平均值。求滿足多重區域條件的函式值,如空白,則返回該單元格。...
Avg函式,函式名。主要用來計算包含在特定查詢欄位中的一組數值的算術平均值。...... Avg函式,函式名。主要用來計算包含在特定查詢欄位中的一組數值的算術平均值。...
均值保留展型(mean-preserving spread MPS)在機率與數理統計中,均值保留展開型的意思是一個機率分布A變化到另外一個機率分布B,B的構成是將A的 機率密度函式 或者...
均值方差理論是指:在確定的情況下,投資者決策可用確定性結果來描述,在風險條件下,任何行動的結果並不被確知,並且結果用頻率函式來表達。頻率函式列示出所有可能...
AVERAGEIF是一個計算機函式,功能是返回某個區域內滿足給定條件的所有單元格的平均值(算術平均值)。如果條件中的單元格為空單元格,AVERAGEIF 就會將其視為 0 值。...
均值估計(mean value estimation)解析數論中的重要概念與方法.即數論函式值的平均估計.由於許多重要的數論函式,其值的分布是很不規則的,所以不能得到其漸近公式....
中文名 均值點 目錄 1 定義 2 套用 均值點定義 編輯 在連續型機率密度函式中,將求得的均值比區間寬度得到的數值即為均值點。均值點套用 編輯 ...
信息函式是用於程式語言中的函式。...... 信息函式是用於程式語言中的函式。常用函式 1、求和函式 SUM 2、平均值函式 AVERAGE 3、邏輯函式 IF 4、捷徑或鏈...
trimmean函式,返回數據集的內部平均值。函式TRIMMEAN 先從數據集的頭部和尾部(最高值和最低值)除去一定百分比的數據點,然後再求平均值。當希望在分析中剔除一部分...
GEOMEAN函式含義 編輯 返回正數數組或區域的幾何平均值。GEOMEAN函式說明 編輯 · 參數可以是數字,或者是包含數字的名稱、數組或引用。...
