基本介紹
定義
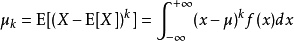

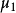
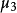
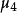
性質



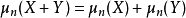
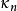
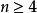
擴展
期望

方差
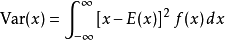
偏態
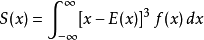
峰態

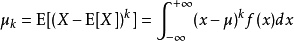

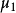
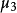
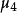



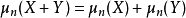
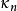
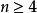

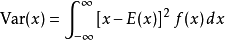
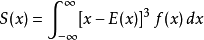

中心矩:對於正整數k,如果E(X)存在,且E[|X-E(X)k]<∞,則稱E{[X-E(X)]k}為隨機變數X的k階中心矩。如X的方差是X的二階中心矩,即D(X)=E{[X-E...
中心動差是指各單位變數值與平均數離差K次方的平均數,也稱為中心矩。中心矩偏態係數是用三階中心動差除以標準差的三次方對比得到,用α3表示。當α3=0時,...
高速加工中心,不斷提高的工作性能是模具製造業得以高效和高精度加工模具的重要前提。在驅動技術的推動下,湧現出結構創新、性能優良的眾多不同類型的高速加工中心。90...
設X是隨機變數,若E(Xk)(k=1,2,...) 存在,則稱它為X的k階原點矩,記作vk(X) 。...... 原點矩與中心矩的關係等等以此類推。原點矩顧名思義,是隨機變...
矩估計,即矩估計法,也稱“矩法估計”,就是利用樣本矩來估計總體中相應的參數。首先推導涉及感興趣的參數的總體矩(即所考慮的隨機變數的冪的期望值)的方程。然後...
矩是一個漢字,讀作ju/jǔ,本意是指曲尺,一種基本工具,可以畫直角形和方形,也可以測度直線長短或估量角度數,也指法度等。該文字在《離騷》和《孟子·離婁上》...
在數學和統計學中,矩(moment)是對變數分布和形態特點的一組度量。n階矩被定義為一變數的n次方與其機率密度函式(Probability Density Function, PDF)之積的積分。...
濃度分布圖形對濃度軸的各階矩量。它用以表示溶質濃度分布的特性。...... 一般用零階矩,一階遠點矩、二至四階中心矩即可描述濃度分布特性。一階矩與零階矩之...
k階矩是數學術語,隸屬於高等數學範疇。...... c=E[X]時,稱為k階中心矩。V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:4次歷史版本 最近更新: 創建者:nih...
設隨機變數的三階矩存在,則稱三階中心矩 除以標準差的三次方 為的偏度係數。偏度係數用以描述常態分配的分布形狀特徵。偏度係數使用標準差為單位計量的偏度係數 ...
設若先將數據標準化,則峰度(係數)相當於標準化數據序列的四階中心矩。所以,在相同的標準差下,峰度係數越大,分布就有更多的極端值,那么其餘值必然要更加集中在...
其中的二階中心矩就是數據的方差,它在一定程度上可以反映分布的峰度,但有時方差相同的數據卻有不同的峰度,因此就利用四階中心矩來反映分布的尖峭程度。為了消除...
