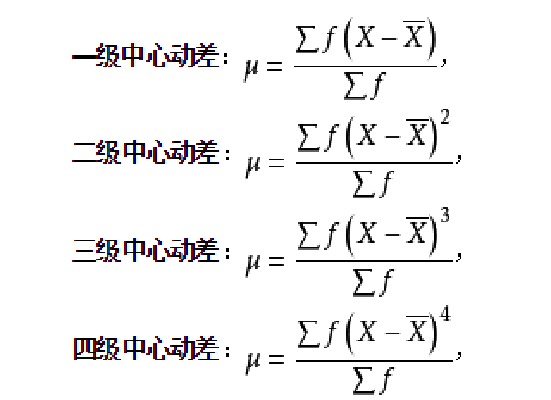中心動差是指各單位變數值與平均數離差K次方的平均數，也稱為中心矩。中心矩偏態係數是用三階中心動差除以標準差的三次方對比得到，用α3表示。當α3=0時，頻數為對稱分布，說明各單位變數值與算術平均數離差三次方後正負值相互抵消；當α3>o時，頻數為右偏分布，α3值越大，右偏斜的程度愈高，說明小於算術平均數的數據次數比大於算術平均數的數據次數多；當α3<0時，頻數為左偏分布，α3值越小，左偏斜的程度愈高，說明大於算術平均數的數據次數比小於算術平均數的數據次數多。
基本介紹
- 中文名：中心動差
- 外文名：central moment
- 所屬學科：數學（統計學）
- 別名：中心矩
- 相關概念：動差，統計動差，偏態係數等
基本介紹,動差與統計動差,中心動差,偏態量與峰態量的度量,數據分布偏態性的測定,峰態量的測定,偏度係數,
基本介紹
動差與統計動差
實際上，差異量的許多指標是來自於動差系統的。動差的概念源於物理學，是指力的力勢(
)，即作用力(
與力臂(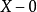
)的乘積，即有
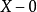
這是因為力的大小是隨力點(
)與原點距離的大小而變化的。在物理學和統計學中，其關係見表1所示。
在統計學中，借用以上物理學中的動勢(或動差)概念而稱為統計動差。用它來表示次數分布的離散情況，其具體思想是把次數分布中的各項次數()視為作用力，把次數分布中的各組觀測值或組中值與原點之差(
)視為距離，由此而得到某一原始分數或某一分組的統計動差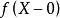
或
。在統計資料中，每一個觀測值或組中值都有其統計動差，對一列觀測值或一個次數分布而言則有其總動差，即
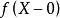
由於總動差受次數分布中次數多少的影響，為了說明一個次數分布中的動差的一般水平，統計學上常把總動差除以總次數稱為平均動差，即
中心動差
統計動差是次數分布對原點的動勢，然而在統計學中，大多數情況下運用的是次數分布對平均數的動勢，即以平均數所在位置為原點，以各組觀測值與均數的差
為力臂，各組次數為作用力來計算動差。這種以均數為原點計算的統計動差叫做中心動差，即
在物理學上，力的動勢分為一，二、三、四級動勢，分別以1、2，3、4次方表示，在統計學中也有相應四級中心動差，它們分別是平均差、方差、偏態量和峰態量的計算依據，即
—級中心動差：
，平均差計平依據；
二級中心動差：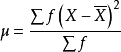
，方差計算公式；
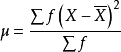
三級中心動差：
，偏態量計算的依據；
四級中心動差：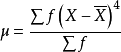
，峰態量計算的依據。
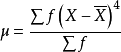
偏態量與峰態量的度量
集中量和差異量能使人們了解一群數據分布的集中趨勢和離中趨勢的情況，但是卻不能告知分布的形態，若要進一步了解分布的形態，則需要了解分布的偏態性與峰態性。
數據分布偏態性的測定
數據分布偏態性測定方法主要有兩種，一是皮爾遜測定法，一是動差測定法。
(一)皮爾遜測定法
皮爾遜測定法是利用均數、中數和眾數之間的關係進行的，其公式為
(二)動差測定法
偏態性的動差測定法是借用中心動差的三級動差進行的，用符號
表示，其公式為
峰態量的測定
峰態量的測定是借用中心動差的四級動差進行的，用符號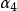
表示，其公式為
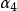
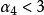
偏度係數
偏度係數是度量頻數分布不對稱程度或偏斜程度的指標。該指標是利用k階中心矩中變數值對平均數正、負離差相互抵消的原理。若頻數分布是完全對稱的，則正、負離差相互抵消，分布沒有偏斜；若頻數分布是左、右偏斜的，那么負離差(正離差)將大於正離差(負離差)，這樣就不會完全抵消，並且偏斜程度越大，中心矩的數值也越大。
一階中心矩和二階中心矩或偶數中心矩都不能用來衡量分布的偏斜程度，因為一階中心矩不論什麼分布都等於0；二階中心矩或偶數中心矩中所有負離差平方後都為正數，無法反映正、負離差的情況。所以，應該選擇三階及以上奇數中心矩作為計算偏度係數的依據。為了簡便，我們選擇以變數的三階中心矩為計算依據，但是考慮到三階中心矩易受單位大小和量綱的影響，所以最終確定將三階中心矩除以標準差的三次方作為衡量分布的偏斜程度，即偏度係數，用符號表示，其公式為
當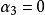
時，頻數分布圍繞平均數左、右兩邊完全對稱，表明頻數分布為正態，如圖1中的A線；
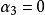
當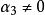
時，頻數分布不對稱，分布有偏斜，的絕對值越大，表示分布的偏斜程度越大，反之亦反；
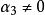
當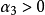
時．大於平均數的標誌值分布較分散，分布曲線向右邊拖長尾巴，稱為右偏(或正偏)，如圖1中的B線；
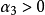
當
時，小於平均數的標誌值分布較分散，分布曲線向左邊拖長尾巴，稱為左偏(或負偏)，如圖1中的C線。
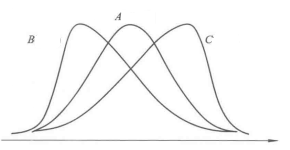圖1 不同偏度的分布曲線圖