基本介紹
含義
四階標準矩
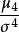


樣本峰度
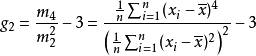
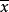
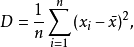

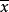

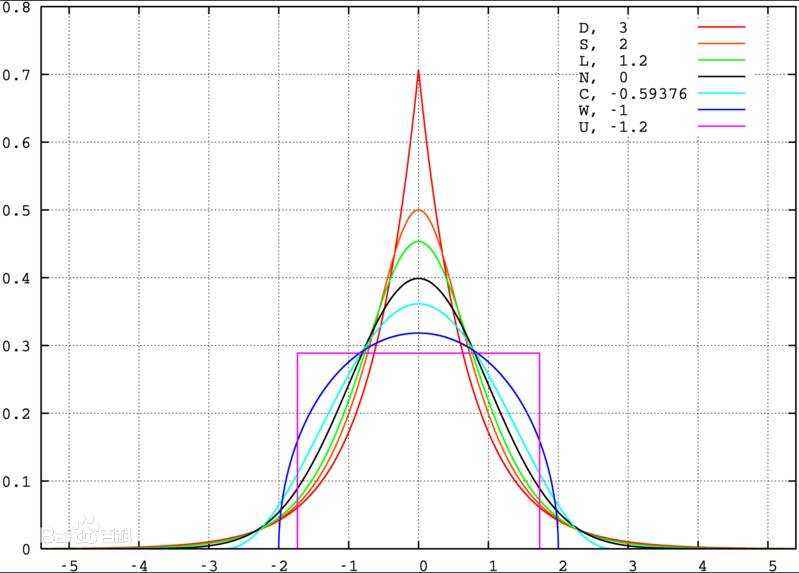

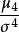


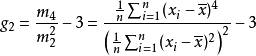
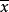
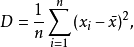

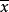

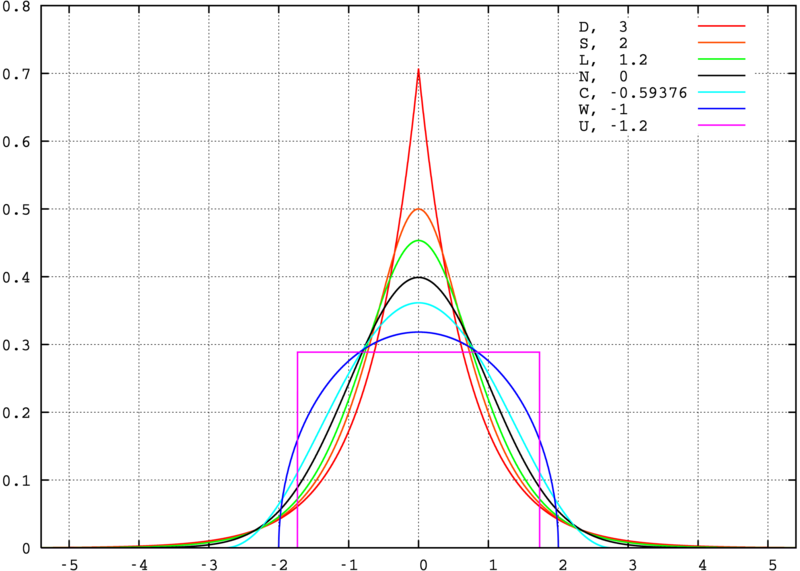
峰度(peakedness;kurtosis)又稱峰態係數。表征機率密度分布曲線在平均值處峰值高低的特徵數。直觀看來,峰度反映了峰部的尖度。樣本的峰度是和常態分配相比較而言...
峰度係數的概念:峰度係數是用來反映頻數分布曲線頂端尖峭或扁平程度的指標。有時兩組數據的算術平均數、標準差和偏態係數都相同,但他們分布曲線頂端的高聳程度卻不...
樣本峰度(sample kurtosis)一種基本統計量,樣本的峰度和偏度都是作為檢驗總體分布正態性的統計量。...
分位數峰度由四分位數和十分位數構造的,單峰分布曲線的“峰”之陡峭程度的一種度量。 ...
江蘇峰度控股集團有限公司於2013年10月15日成立。法定代表人駱國峰,公司經營範圍包括:實業投資;房地產開發;房產信息諮詢服務;房屋中介服務;物業管理服務等。...
樣本分位數峰度(sample quantile kurtosis)是指將分位數峰度中的分位數換成相應的樣本分位數所得的統計量。分位數峰度是由四分位數和十分位數構造的,單峰分布...
常州峰度房地產諮詢有限公司於2013年10月15日在常州市武進區市場監督管理局登記成立。法定代表人駱國峰,公司經營範圍包括房地產投資、諮詢及企業形象策劃。(依法須經...
佛山市中裕峰度陶瓷有限公司於2017年06月08日成立。法定代表人許振海,公司經營範圍包括:銷售:陶瓷製品、建築材料、衛生潔具及配件等。...
杭州峰度健身管理有限公司於2014年12月26日在杭州市下城區市場監督管理局登記成立。法定代表人李帥,公司經營範圍包括一般經營項目:服務:健身管理,健身諮詢,企業管理...
御園4期峰度“一座長在園林中的風景別墅!”由揚州虹源房地產開發有限公司(台灣虹源集團子公司)開發,清華大學建築設計院設計。地處潤揚北路18號,位於蜀岡風景區西...
1 偏度簡介 2 計算 3 峰度 偏度偏度簡介 編輯 偏度(skewness),是統計數據分布偏斜方向和程度的度量,是統計數據分布非對稱程度的數字特徵。偏度(Skewness)亦稱偏...
在機率論中,厚尾即肥尾,肥尾分布(英語:Fat-tailed distribution)是一種機率分布模型。它是一種重尾分布,但是它的偏度或峰度極端的大。與無所不在的常態分配作...
偏態分布是與“常態分配”相對,分布曲線左右不對稱的數據次數分布,是連續隨機變數機率分布的一種。可以通過峰度和偏度的計算,衡量偏態的程度。可分為正偏態和負...
峰態係數( coefficient of kurtosis)即“峰度”。設隨機變數X的數學期望與方差統計學分別為EX和var(x)≠o,則稱≤萇:毒籌£一3為x的峰度。它是反映X的密度...
其中,n為樣本容量,S為偏度,K為峰度。在常態分配的假設下,JB統計量漸進地服從自由度為2的卡方分布, JBasy~χ2(2)。若變數服從常態分配,則S為零,K為3,...
常用的正態性檢驗方法有正態機率紙法、夏皮羅維爾克檢驗法(Shapiro-Wilktest),科爾莫戈羅夫檢驗法,偏度-峰度檢驗法等。正態性檢驗問題為: 總體服從常態分配 : ...
