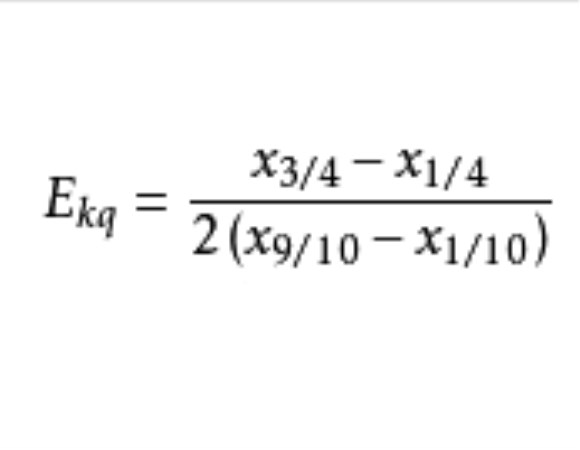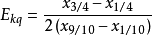基本介紹
- 中文名：樣本分位數峰度
- 外文名：sample quantile kurtosis
- 所屬學科：數學（統計學）
- 所屬問題：統計學（機率論）
- 相關概念：分位數峰度，四分位數，十分位數
基本介紹,峰度及測度,樣本峰度,矩法,分位數法,
基本介紹
設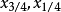
和
相應為隨機變數X的上、下四分位數和上、下十分位數，則稱
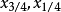
峰度及測度
在社會經濟現象中，許多變數數列的曲線與常態分配的曲線相比，其頂部的形態會有所不同，即分布圖形的尖峭程度或扁平程度有所不同。如果一個總體在眾數周圍集中的程度很高，其分布的圖形就會比較陡峭；反之，如果總體在眾數周圍的集中程度較低，其分布的圖形就會比較平坦。峰度指標就是反映這方面的分布情況的一個數值特徵。
樣本峰度
對於具有n個值的樣本，樣本峰度為：
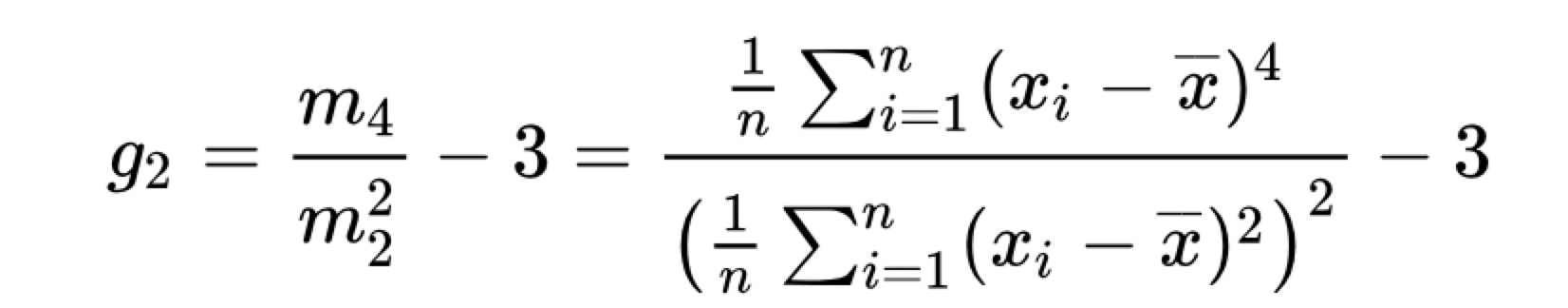
其中m4是四階樣本中心矩，m2是二階中心矩（樣本方差），xi是第i個值，X bar是樣本平均值。注意此處計算方差的時候除數是N，而不是單獨計算樣本方差的(N-1)。
另有公式：
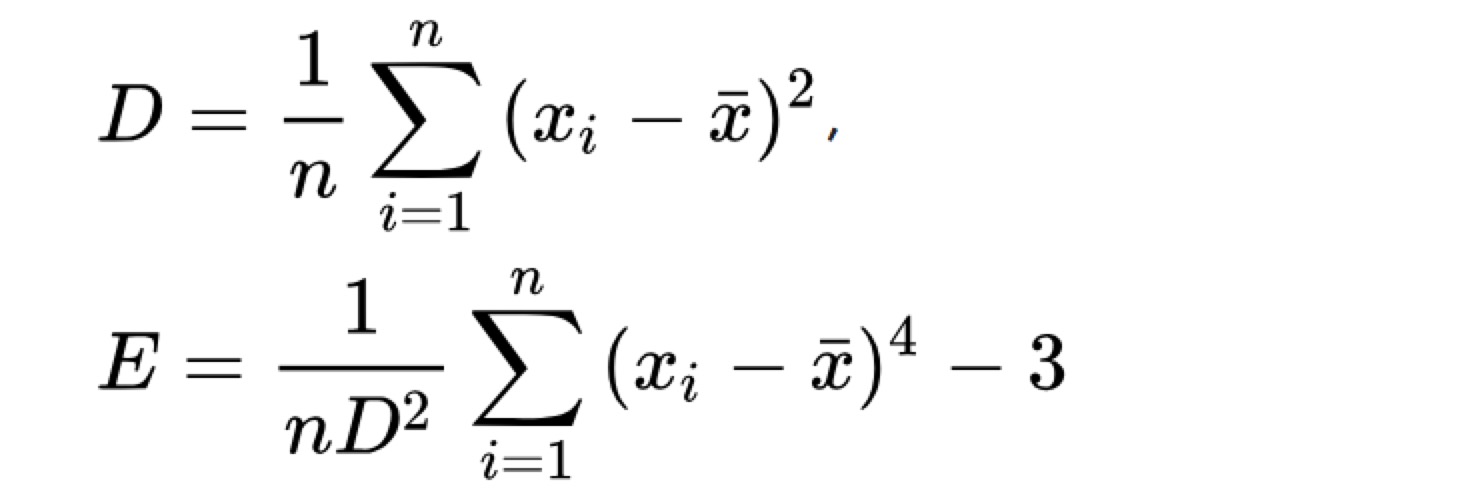
其中，n為樣本大小，D為事先計算的方差，xi是第i個值，X bar是樣本算術平均值。
在統計軟體如Excel中，計算樣本的峰度公式如下：
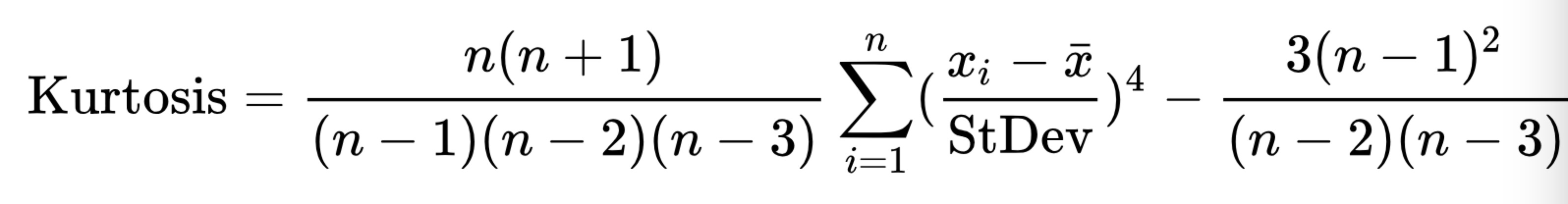
矩法
在一般情況下，總體分布圖形的陡峭程度與偶數階中心矩的數值大小有關。如偶數階中心矩的數值越大，分布圖形越平坦；數值越小，分布圖形越尖峭。如果將分布的四階中心矩與標準差的四次方對比，得到的數值大小與峰度的高低能夠保持一致，同時又恰好消除了計量單位對計算結果的影響。由此形成了峰度指標的基本構造方式。但對於常態分配，這樣計算的結果恆為一個常數：
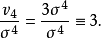
因此，可以將各種分布的峰凸程度都與常態分配相比，得到峰度的標準測定公式：
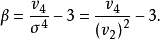
當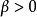
時，分布為高峰度
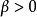
當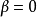
時，分布為常態分配
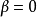
當
時，分布為低峰度
這裡所說的峰度高、低，都是與具有相同標準差或方差的常態分配比較而言的。
分位數法
為了排除極端值的干擾，分布的峰度也可以採用分位數的方法來測定。例如，人們常利用上、下兩個四分位數和上、下兩個十分位數之間的數量關係來衡量峰度：
觀察表明，計算得到的數值越小，分布圖形越陡峭；反之，數值越大，分布圖形越平坦。理論上可以證明，對於常態分配，這樣計算的結果總是0.526，故可以定義相應的“分位數峰度”指標為
